
【题目】设有关于x的一元二次方程![]() .
.
![]() 若a是从0,1,2三个数中任取的一个数,b是从0,1,2,3四个数中任取的一个数,求上述方程有实根的概率;
若a是从0,1,2三个数中任取的一个数,b是从0,1,2,3四个数中任取的一个数,求上述方程有实根的概率;
![]() 若a是从区间
若a是从区间![]() 任取的一个数,b是从区间
任取的一个数,b是从区间![]() 任取的一个数,求上述方程有实数的概率.
任取的一个数,求上述方程有实数的概率.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
首先分析一元二次方程有实根的条件,得到a≥b
(1)本题是一个古典概型,试验发生包含的基本事件可以通过列举得到结果数,满足条件的事件在前面列举的基础上得到结果数,求得概率.
(2)本题是一个几何概型,试验的全部结果所构成的区域为{(a,b)|0≤a≤2,0≤b≤3},满足条件的构成事件A的区域为{(a,b)|0≤a≤2,0≤b≤3,a≥b},根据概率等于面积之比,得到概率.
设事件A为“方程有实根”.
当a>0,b>0时,方程有实根的充要条件为a≥b
(1)由题意知本题是一个古典概型,试验发生包含的基本事件共12个:
(0,0)(0,1)(0,2)(0,3)(1,0)(1,1)(1,2)(1,3)(2,0)(2,1)(2,2)(2,3)
其中第一个数表示a的取值,第二个数表示b的取值.
事件A中包含6个基本事件,
∴事件A发生的概率为P![]() ;
;
(2)由题意知本题是一个几何概型,
试验的全部结果所构成的区域为{(a,b)|0≤a≤2,0≤b≤3}
满足条件的构成事件A的区域为{(a,b)|0≤a≤2,0≤b≤3,a≥b}
∴所求的概率是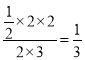 .
.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:
【题目】已知公差不为![]() 的等差数列
的等差数列![]() 的首项为1,前
的首项为1,前![]() 项和为
项和为![]() ,且数列
,且数列![]() 是等差数列.
是等差数列.
(1)求数列![]() 的通项公式;
的通项公式;
(2)设![]() ,问:
,问:![]()
![]() 均为正整数,且
均为正整数,且![]() 能否成等比数列?若能,求出所有的
能否成等比数列?若能,求出所有的![]() 和
和![]() 的值;若不能,请说明理由.
的值;若不能,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司计划在迎春节联欢会中设一项抽奖活动:在一个不透明的口袋中装入外形一样号
码分别为1,2,3,…,10的十个小球。活动者一次从中摸出三个小球,三球号码有且仅有两个连号的为三等奖,奖金30元;三球号码都连号为二等奖,奖金60元;三球号码分别为1,5,10为一等奖,奖金240元;其余情况无奖金。
(1)求员工甲抽奖一次所得奖金ξ的分布列与期望;
(2)员工乙幸运地先后获得四次抽奖机会,他得奖次数![]() 的方差是多少?
的方差是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】铁人中学高二学年某学生对其亲属30人![]() 饮食习惯进行了一次调查,并用如图所示的茎叶图表示30人的饮食指数.(说明:图中饮食指数低于70的人,饮食以蔬菜为主;饮食指数高于70的人,饮食以肉类为主.)
饮食习惯进行了一次调查,并用如图所示的茎叶图表示30人的饮食指数.(说明:图中饮食指数低于70的人,饮食以蔬菜为主;饮食指数高于70的人,饮食以肉类为主.)
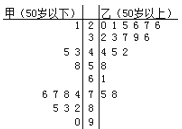
(Ⅰ)根据茎叶图,帮助这位学生说明其亲属30人的饮食习惯;
(Ⅱ)根据以上数据完成下列![]() 的列联表:
的列联表:
主食蔬菜 | 主食肉类 | 合计 | |
50岁以下人数 | |||
50岁以上人数 | |||
合计人数 |
(Ⅲ)能否在犯错误的概率不超过0.01的前提下认为其亲属的饮食习惯与年龄有关系?
附:![]() .
.
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出如下四个命题:①若“![]() 且
且![]() ”为假命题,则
”为假命题,则![]() 均为假命题;②命题“若
均为假命题;②命题“若![]() ,则
,则![]() ”的否命题为“若
”的否命题为“若![]() ,则
,则![]() ”; ③“
”; ③“![]() ,则
,则![]() ”的否定是“
”的否定是“![]() ,则
,则![]() ”;④在
”;④在![]() 中,“
中,“![]() ”是“
”是“![]() ”的充要条件.其中正确的命题的个数是( )
”的充要条件.其中正确的命题的个数是( )
A. 1B. 2C. 3D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com