
| 2 |
| π |
| 2 |
| π |
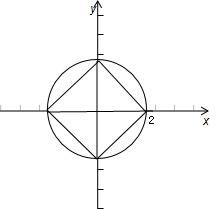 解:如图所示,满足条件:“|x|+|y|≤2”的区域Ω为图中正方形,
解:如图所示,满足条件:“|x|+|y|≤2”的区域Ω为图中正方形,| 2 |
| 8 |
| 4π |
| 2 |
| π |
| 2 |
| π |
| N(A) |
| N |


科目:高中数学 来源:2011-2012学年福建省福州市高三第一学期期末质量检测理科数学 题型:填空题
在圆x2+y2=4所围成的区域内随机取一个点P(x,y),则| x |+| y | ≤ 2的概率为 .
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江苏省、海门中学、天一中学高三联考数学 题型:填空题
在圆x2+y2=4所围成的区域内随机取一个点P(x,y),则| x |+| y | ≤ 2的概率为 ▲ .
查看答案和解析>>
科目:高中数学 来源:2012-2013学年江苏省徐州市诚贤中学高三(上)第二次质量检测数学试卷(解析版) 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2011-2012学年福建省福州市高三(上)期末数学试卷(理科)(解析版) 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com