
分析 (1)由点P(m,m+1)在圆上,可得m的方程,解方程可得;
(2)由(1)配方可得圆C:(x-2)2+(y-7)2=8,可得$r=2\sqrt{2}$,$|{CQ}|=4\sqrt{2}$,结合图象易得最值;
(3)设$E({-3,3}),k=\frac{b-3}{a+3}$,当过点E的直线与圆相切时,k取最大值,结合点到直线的距离公式可得.
解答 解:(1)∵点P(m,m+1)在圆上,
∴m2+(m+1)2-4m-14(m+1)+45=0
解得m=4,∴P(4,5),
∴kPQ=$\frac{3-5}{-2-4}$=$\frac{1}{3}$;
(2)由(1)配方可得圆C:(x-2)2+(y-7)2=8,
∴$r=2\sqrt{2}$,$|{CQ}|=4\sqrt{2}$,∴${|{MQ}|_{max}}=|{CQ}|+r=6\sqrt{2}$,
${|{MQ}|_{min}}=|{CQ}|-r=2\sqrt{2}$;
(3)设$E({-3,3}),k=\frac{b-3}{a+3}$,
如图,当过点E的直线与圆相切时,k取最大值.
∵切线方程为y-3=k(x+3),即kx-y+3k+3=0
∴$d=\frac{{|{5k-4}|}}{{\sqrt{{k^2}+1}}}=2\sqrt{2}$,∴$k=\frac{{20±2\sqrt{66}}}{17}$,
∴$\frac{b-3}{a+3}$的最大值为$\frac{{20+2\sqrt{66}}}{17}$.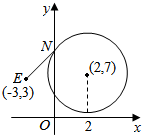
点评 本题考查直线和圆的位置关系,数形结合是解决问题的关键,属中档题.


科目:高中数学 来源: 题型:选择题
| A. | 120°角与420°角的终边相同 | |
| B. | 若α是锐角.则2α是第二象限的角 | |
| C. | -240°角与480°角都是第三象限的角 | |
| D. | 60°角与-420°角的终边关于x轴对称 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{π}$ | B. | (3-2$\sqrt{2}$)π | C. | $\frac{1}{π}$ | D. | $\frac{1}{2π}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 只有一个 | B. | 只有两个 | C. | 至多3个 | D. | 有无数个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com