
分析 (1)求出函数的导数,从而求出函数的单调区间即可;
(2)设直线l和曲线y=lnx,(x>1),y=ex都相切,切点是(x1,y1),(x2,y2),得到lnx1=$\frac{{x}_{1}+1}{{x}_{1}-1}$,(x1>1)有唯一解,从而证出结论.
解答 解:(1)f′(x)=$\frac{1}{x}$+$\frac{a+1}{{(x-1)}^{2}}$,由f′(2)=$\frac{5}{2}$,解得:a=1,
f′(x)=$\frac{1}{x}$+$\frac{2}{{(x-1)}^{2}}$=$\frac{{x}^{2}+1}{x{•(x-1)}^{2}}$,
∵x>0且x≠1,∴f′(x)>0,
∴函数f(x)的递增区间是(0,1)和(1,+∞);
(2)证明:设直线l和曲线y=lnx,(x>1),
y=ex都相切,切点是(x1,y1),(x2,y2),
∵y′=$\frac{1}{x}$,∴y′${|}_{x{=x}_{1}}$=$\frac{1}{{x}_{1}}$,
∴曲线y=lnx在x=x1处的曲线方程是y-lnx1=$\frac{1}{{x}_{1}}$(x-x1),
即y=$\frac{1}{{x}_{1}}$x+lnx1-1,①,
∵y′=${e}^{{x}_{2}}$,∴${e}^{{x}_{2}}$=$\frac{1}{{x}_{1}}$,∴x2=-lnx1,
∴直线l也是y-$\frac{1}{{x}_{2}}$=$\frac{1}{{x}_{1}}$(x+lnx1),
即y=$\frac{1}{{x}_{2}}$x+$\frac{l{nx}_{2}}{{x}_{1}}$+$\frac{1}{{x}_{2}}$②,
由①②得lnx1-1=$\frac{l{nx}_{1}}{{x}_{1}}$+$\frac{1}{{x}_{1}}$,
∴lnx1=$\frac{{x}_{1}+1}{{x}_{1}-1}$,x1>1
由(1)得,f(x)=lnx-$\frac{x+1}{x-1}$在(1,+∞)递增,
又f(e)=lne-$\frac{e+1}{e-1}$=-$\frac{2}{e-1}$<0,f(e2)=$\frac{{e}^{2}-3}{{e}^{2}-1}$>0,
根据零点存在定理得方程f(x)=0必在区间(e,e2)上有唯一的根,
即方程lnx1=$\frac{{x}_{1}+1}{{x}_{1}-1}$,x1>1有唯一的解.
点评 本题考查了函数的单调性.最值问题,考查导数的应用以及零点判断定理,是一道中档题.


科目:高中数学 来源: 题型:选择题
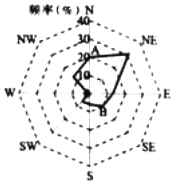 如图所示为某城市去年风向频率图,图中A点表示该城市去年有的天数吹北风,点表示该城B市去年有10%的天数吹东南风,下面叙述不正确的是( )
如图所示为某城市去年风向频率图,图中A点表示该城市去年有的天数吹北风,点表示该城B市去年有10%的天数吹东南风,下面叙述不正确的是( )| A. | 去年吹西北风和吹东风的频率接近 | B. | 去年几乎不吹西风 | ||
| C. | 去年吹东风的天数超过100天 | D. | 去年吹西南风的频率为15%左右 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
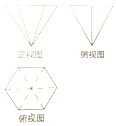 一个几何体的三视图如图所示,其中正视图是边长为2的等边三角形,俯视图为正六边形,则该几何体的体积是( )
一个几何体的三视图如图所示,其中正视图是边长为2的等边三角形,俯视图为正六边形,则该几何体的体积是( )| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com