
【题目】某公司为了预测下月产品销售情况,找出了近7个月的产品销售量![]() (单位:万件)的统计表:
(单位:万件)的统计表:
月份代码 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
销售量 |
|
|
|
|
|
|
|
但其中数据污损不清,经查证![]() ,
,![]() ,
,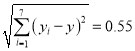 .
.
(1)请用相关系数说明销售量![]() 与月份代码
与月份代码![]() 有很强的线性相关关系;
有很强的线性相关关系;
(2)求![]() 关于
关于![]() 的回归方程(系数精确到0.01);
的回归方程(系数精确到0.01);
(3)公司经营期间的广告宣传费![]() (单位:万元)(
(单位:万元)(![]() ),每件产品的销售价为10元,预测第8个月的毛利润能否突破15万元,请说明理由.(毛利润等于销售金额减去广告宣传费)
),每件产品的销售价为10元,预测第8个月的毛利润能否突破15万元,请说明理由.(毛利润等于销售金额减去广告宣传费)
参考公式及数据:![]() ,相关系数
,相关系数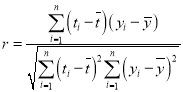 ,当
,当![]() 时认为两个变量有很强的线性相关关系,回归方程
时认为两个变量有很强的线性相关关系,回归方程![]() 中斜率和截距的最小二乘估计公式分别为
中斜率和截距的最小二乘估计公式分别为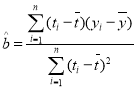 ,
,![]() .
.
科目:高中数学 来源: 题型:
【题目】一个工厂在某年里连续10个月每月产品的总成本![]() (万元)与该月产量
(万元)与该月产量![]() (万件)之间有如下一组数据:
(万件)之间有如下一组数据:
| 1.08 | 1.12 | 1.19 | 1.28 | 1.36 | 1.48 | 1.59 | 1.68 | 1.80 | 1.87 |
| 2.25 | 2.37 | 2.40 | 2.55 | 2.64 | 2.75 | 2.92 | 3.03 | 3.14 | 3.26 |
(1)通过画散点图,发现可用线性回归模型拟合![]() 与
与![]() 的关系,请用相关系数
的关系,请用相关系数![]() 加以说明;
加以说明;
(2)①建立月总成本![]() 与月产量
与月产量![]() 之间的回归方程;②通过建立的
之间的回归方程;②通过建立的![]() 关于
关于![]() 的回归方程,估计某月产量为1.98万件时,产品的总成本为多少万元?(均精确到0.001)
的回归方程,估计某月产量为1.98万件时,产品的总成本为多少万元?(均精确到0.001)
附注:①参考数据:![]() ,
,![]() ,
,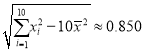 ,
,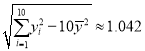 ,
,![]() .
.
②参考公式:相关系数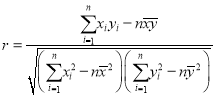 ,
,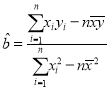 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“微信运动”已成为当下热门的运动方式,小王的微信朋友内也有大量好友参与了“微信运动”,他随机选取了其中的40人(男、女各20人),记录了他们某一天的走路步数,并将数据整理如下:
性别 步数 | 0~2000 | 2001~5000 | 5001~8000 | 8001~10000 | >10000 |
男 | 1 | 2 | 3 | 6 | 8 |
女 | 0 | 2 | 10 | 6 | 2 |
(1)已知某人一天的走路步数超过8000步被系统评定为“积极型”,否则为“懈怠型”,根据题意完成下面的2×2列联表,并据此判断能否有95%以上的把握认为“评定类型”与“性别”有关?
积极型 | 懈怠型 | 总计 | |
男 | |||
女 | |||
总计 |
(2)若小王以这40位好友该日走路步数的频率分布来估计其所有微信好友每日走路步数的概率分布,现从小王的所有微信好友中任选2人,其中每日走路不超过5000步的有X人,超过10000步的有Y人,设ξ=|X﹣Y|,求E的分布列及数学期望.
附:K2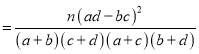 ,n=a+b+c+d.
,n=a+b+c+d.
P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左顶点为
的左顶点为![]() ,右焦点为
,右焦点为![]() ,过
,过![]() 作垂直于
作垂直于![]() 轴的直线交该椭圆于
轴的直线交该椭圆于![]() ,
,![]() 两点,直线
两点,直线![]() 的斜率为
的斜率为![]() .
.
(Ⅰ)求椭圆的离心率;
(Ⅱ)若![]() 的外接圆在
的外接圆在![]() 处的切线与椭圆交另一点于
处的切线与椭圆交另一点于![]() ,且
,且![]() 的面积为
的面积为![]() ,求椭圆的方程.
,求椭圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
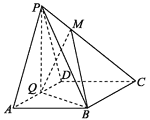
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为菱形,
为菱形,![]() 为
为![]() 的中点,
的中点,![]() .
.
(1)求证:![]() 平面
平面![]() ;
;
(2)点![]() 在线段
在线段![]() 上,
上,![]() ,试确定
,试确定![]() 的值,使
的值,使![]() 平面
平面![]() ;
;
(3)若![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,求二面角
,求二面角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某气象站统计了4月份甲、乙两地的天气温度(单位![]() ),统计数据的茎叶图如图所示,
),统计数据的茎叶图如图所示,
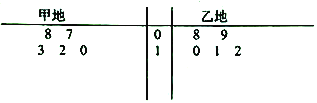
(1)根据所给茎叶图利用平均值和方差的知识分析甲,乙两地气温的稳定性;
(2)气象主管部门要从甲、乙两地各随机抽取一天的天气温度,若甲、乙两地的温度之和大于或等于![]() ,则被称为“甲、乙两地往来温度适宜天气”,求“甲、乙两地往来温度适宜天气”的概率.
,则被称为“甲、乙两地往来温度适宜天气”,求“甲、乙两地往来温度适宜天气”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知顶点是坐标原点的抛物线![]() 的焦点
的焦点![]() 在
在![]() 轴正半轴上,圆心在直线
轴正半轴上,圆心在直线![]() 上的圆
上的圆![]() 与
与![]() 轴相切,且
轴相切,且![]() 关于点
关于点![]() 对称.
对称.
(1)求![]() 和
和![]() 的标准方程;
的标准方程;
(2)过点![]() 的直线
的直线![]() 与
与![]() 交于
交于![]() ,与
,与![]() 交于
交于![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com