
【题目】如图,已知四棱锥P﹣ABCD的底面为菱形,∠BCD=120°,AB=PC=2,AP=BP= ![]() .
. 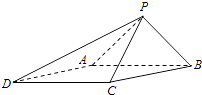
(1)求证:AB⊥PC;
(2)求二面角B一PC﹣D的余弦值.
【答案】
(1)证明:取AB的中点O,连接PO,CO,AC,
∵△APB为等腰三角形,∴PO⊥AB
又∵四边形ABCD是菱形,∠BCD=120°,
∴△ACB是等边三角形,∴CO⊥AB
又CO∩PO=O,∴AB⊥平面PCO,
又PC平面PCO,∴AB⊥PC
(2)解:∵ABCD为菱形,∠BCD=120°,AB=PC=2,AP=BP= ![]() ,
,
∴PO=1,CO= ![]() ,∴OP2+OC2=PC2,
,∴OP2+OC2=PC2,
∴OP⊥OC,
以O为原点,OC为x轴,OB为y轴,OP为z轴,
建立空间直角坐标系,
则A(0,﹣1,0),B(0,1,0),C( ![]() ,0,0),
,0,0),
P(0,0,1),D( ![]() ,﹣2,0),
,﹣2,0),
![]() =(
=( ![]() ,﹣1,0),
,﹣1,0), ![]() =(
=( ![]() ,0,-1),
,0,-1), ![]() =(0,2,0),
=(0,2,0),
设平面DCP的法向量 ![]() =(x,y,z),
=(x,y,z),
则 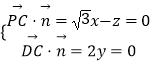 ,令x=1,得
,令x=1,得 ![]() =(1,0,
=(1,0, ![]() ),
),
设平面PCB的法向量 ![]() =(a,b,c),
=(a,b,c),
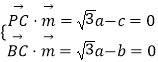 ,令a=1,得
,令a=1,得 ![]() =(1,
=(1, ![]() ,
, ![]() ),
),
cos< ![]() >=
>= ![]() =
= ![]() ,
,
∵二面角B一PC﹣D为钝角,∴二面角B一PC﹣D的余弦值为﹣ ![]() .
.
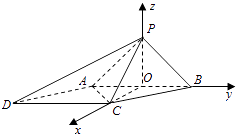
【解析】(1)取AB的中点O,连接PO,CO,AC,由已知条件推导出PO⊥AB,CO⊥AB,从而AB⊥平面PCO,由此能证明AB⊥PC.(2)由已知得OP⊥OC,以O为原点,OC为x轴,OB为y轴,OP为z轴,建立空间直角坐标系,利用向量法能求出二面角B一PC﹣D的余弦值.
【考点精析】关于本题考查的空间中直线与直线之间的位置关系,需要了解相交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点;异面直线: 不同在任何一个平面内,没有公共点才能得出正确答案.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知{an}是单调递增的等差数列,首项a1=3,前n项和为Sn , 数列{bn}是等比数列,首项b1=1,且a2b2=12,S3+b2=20.
(1)求{an}和{bn}的通项公式.
(2)令Cn=nbn(n∈N+),求{cn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(x﹣1)2+a(lnx﹣x+1)(其中a∈R,且a为常数)
(1)若对于任意的x∈(1,+∞),都有f(x)>0成立,求a的取值范围;
(2)在(1)的条件下,若方程f(x)+a+1=0在x∈(0,2]上有且只有一个实根,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)= ![]() sinxcsox+cos2x+m
sinxcsox+cos2x+m
(1)求函数f(x)的最小正周期和单调递增区间;
(2)当x∈[﹣ ![]() ,
, ![]() ]时,函数f(x)的最小值为2,求函数f(x)的最大值及对应的x的值.
]时,函数f(x)的最小值为2,求函数f(x)的最大值及对应的x的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种药种植基地有两处种植区的药材需在下周一、周二两天内采摘完毕,基地员工一天可以完成一处种植区的采摘,由于下雨会影响药材的收益,若基地收益如下表所示:已知下周一和下周二无雨的概率相同且为![]() ,两天是否下雨互不影响,若两天都下雨的概率为
,两天是否下雨互不影响,若两天都下雨的概率为![]()

(1)求![]() 及基地的预期收益;
及基地的预期收益;
(2)若该基地额外聘请工人,可在周一当天完成全部采摘任务,若周一无雨时收益为![]() 万元,有雨时收益为
万元,有雨时收益为![]() 万元,且额外聘请工人的成本为
万元,且额外聘请工人的成本为![]() 元,问该基地是否应该额外聘请工人,请说明理由.
元,问该基地是否应该额外聘请工人,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合M={(x,y)||x|≤2,|y|≤1},在集合M内随机取出一个元素(x,y).
(1)求以(x,y)为坐标的点落在圆x2+y2=1内的概率.
(2)若x,y都是整数,求以(x,y)为坐标的点落在圆x2+y2=1内或该圆上的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,根据下列条件解三角形,则其中有两个解的是( )
A.b=10,A=45°,B=60°
B.a=60,c=48,B=120°
C.a=7,b=5,A=75°
D.a=14,b=16,A=45°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国是世界上严重缺水的国家,某市政府为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准x(吨),一位居民的月用水量不超过x的部分按平价收费,超出x的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5)分成9组,制成了如图所示的频率分布直方图. 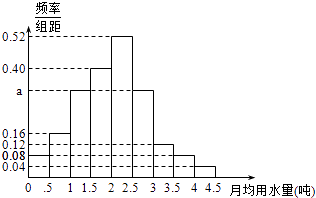
(Ⅰ)求直方图中a的值;
(Ⅱ)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数,并说明理由;
(Ⅲ)若该市政府希望使85%的居民每月的用水量不超过标准x(吨),估计x的值,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com