
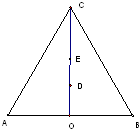
 如图,在等边△ABC中,O为边AB的中点,AB=4,D、E为△ABC的高线上的点,且|
如图,在等边△ABC中,O为边AB的中点,AB=4,D、E为△ABC的高线上的点,且|| OC |
| 3 |
| OD |
| OC |
| 3 |
| OE |
| EP |
| EQ |
| EP |
| EQ |
| EP |
| EP |
| EP |
| EQ |
| OC |
| 3 |
| OD |
| OC |
| 3 |
| OE |
| OD |
| 1 | ||
2
|
| OC |
| OE |
| 1 | ||
|
| OC |
| x2 |
| a2 |
| y2 |
| b2 |
| 5 |
| x2 |
| 5 |
| EP |
| EQ |
| EQ |
| EP |
|
|
|
|
| y | 2 2 |
| 5λ-3 |
| 4λ |
| 1 |
| 3 |
| EP |
| EQ |
| 1 |
| 3 |


科目:高中数学 来源:2012-2013学年江苏省仪征市高三第一次涂卡训练数学试卷(解析版) 题型:填空题
如图,在等边△ABC中,P是边AC上一点,连接BP,将△BCP绕点B逆时针旋转60°,得到△BAQ,连接PQ.若BC=8,BP=7,则△APQ的周长是 .
查看答案和解析>>
科目:高中数学 来源:2011年甘肃省兰州一中高考数学三模试卷(文科)(解析版) 题型:解答题
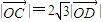 ,
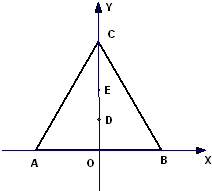
, .若以A,B为焦点,O为中心的椭圆过点D,建立适当的直角坐标系,记椭圆为M.
.若以A,B为焦点,O为中心的椭圆过点D,建立适当的直角坐标系,记椭圆为M.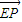 =λ
=λ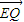 ,求实数λ的取值范围.
,求实数λ的取值范围.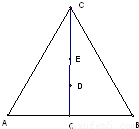
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com