
【题目】设![]() ,若函数
,若函数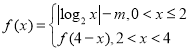 有4个不同的零点
有4个不同的零点![]() ,且
,且![]() ,则
,则![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
先求出函数的解析式,根据题意,由零点,可以得方程,然后常变量分离,构造函数,利用新构造函数的对称性,得到![]() 之间的关系,再根据对数的运算性质,得到
之间的关系,再根据对数的运算性质,得到![]() 之间的关系,这样可以把
之间的关系,这样可以把![]() 化简成关于
化简成关于![]() 的代数式,最后利用换元法,基本不等式以及函数的单调性求出值域即可.
的代数式,最后利用换元法,基本不等式以及函数的单调性求出值域即可.
当![]() 时,所以有
时,所以有![]() ,因此有
,因此有![]() ,所以函数的解析式为:
,所以函数的解析式为: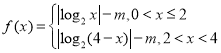 ,由题意可知:
,由题意可知:![]() 有四个不同的实数解,因此有:
有四个不同的实数解,因此有: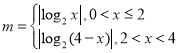 ,设函数
,设函数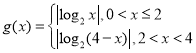 ,因此由可知:函数
,因此由可知:函数![]() 的图象与函数
的图象与函数![]() 的图象有四个不同的交点,函数
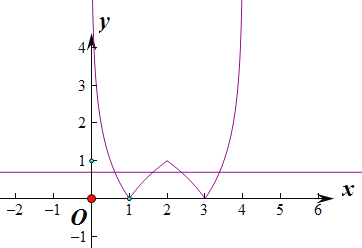
的图象有四个不同的交点,函数![]() 的图象如下图所示:
的图象如下图所示:
要想函数![]() 的图象与函数
的图象与函数![]() 的图象有四个不同的交点,必须有
的图象有四个不同的交点,必须有![]() ,此时有
,此时有![]() ,再由
,再由![]() ,结合图象可知:
,结合图象可知:![]() 函数是关于直线
函数是关于直线![]() 对称,因此有
对称,因此有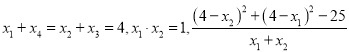
![]() ,所以
,所以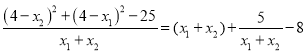 ,令
,令![]() ,令
,令![]() ,显然函数在
,显然函数在![]() 上单调递减,
上单调递减,
在![]() 上单调递增,
上单调递增,
故![]() ,
,![]() .
.
故选:A


科目:高中数学 来源: 题型:
【题目】如图,四棱柱ABCD-![]() 中,地面ABCD为直角梯形,AB∥CD,AB⊥BC,平面ABCD⊥平面AB
中,地面ABCD为直角梯形,AB∥CD,AB⊥BC,平面ABCD⊥平面AB![]() ,∠BA
,∠BA![]() =60°,AB=A
=60°,AB=A![]() =2BC=2CD=2
=2BC=2CD=2
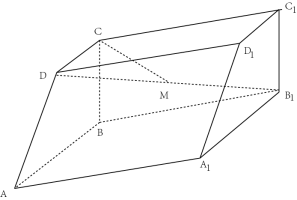
(1)求证:BC⊥A![]() ;
;
(2)求二面角D-A![]() -B的余弦值;
-B的余弦值;
(3)在线段D![]() 上是否存在点M,使得CM∥平面DA
上是否存在点M,使得CM∥平面DA![]() ?若存在,求
?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代数学名著《九章算术》中有这样一个问題:今有牛、马、羊食人苗,苗主责之粟五斗,羊主曰:“我羊食半马、“马主曰:“我马食半牛,”今欲衰偿之,问各出几何?此问题的译文是:今有牛、马、羊吃了别人的禾苗,禾苗主人要求赔偿5斗粟、羊主人说:“我羊所吃的禾苗只有马的一半,”马主人说:“我马所吃的禾苗只有牛的一半,“打算按此比例偿还,他们各应偿还多少?该问题中,1斗为10升,则马主人应偿还( )升粟?
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左、右顶点分别为C、D,且过点
的左、右顶点分别为C、D,且过点![]() ,P是椭圆上异于C、D的任意一点,直线PC,PD的斜率之积为
,P是椭圆上异于C、D的任意一点,直线PC,PD的斜率之积为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)O为坐标原点,设直线CP交定直线x = m于点M,当m为何值时,![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定点![]() ,圆
,圆![]() ,点
,点![]() 为圆
为圆![]() 上动点,线段
上动点,线段![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() ,记
,记![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)过点![]() 与
与![]() 作平行直线
作平行直线![]() 和
和![]() ,分别交曲线
,分别交曲线![]() 于点
于点![]() 、
、![]() 和点
和点![]() 、
、![]() ,求四边形
,求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国大学先修课程,是在高中开设的具有大学水平的课程,旨在让学有余力的高中生早接受大学思维方式、学习方法的训练,为大学学习乃至未来的职业生涯做好准备.某高中开设大学先修课程已有两年,两年共招收学生2000人,其中有300人参与学习先修课程,两年全校共有优等生200人,学习先修课程的优等生有60人.这两年学习先修课程的学生都参加了考试,并且都参加了某高校的自主招生考试(满分100分),结果如下表所示:
分数 |
|
|
|
|
|
人数 | 20 | 55 | 105 | 70 | 50 |
参加自主招生获得通过的概率 | 0.9 | 0.8 | 0.6 | 0.5 | 0.4 |
(1)填写列联表,并画出列联表的等高条形图,并通过图形判断学习先修课程与优等生是否有关系,根据列联表的独立性检验,能否在犯错误的概率不超过0.01的前提下认为学习先修课程与优等生有关系?
优等生 | 非优等生 | 总计 | |
学习大学先修课程 | |||
没有学习大学先修课程 | |||
总计 |
(2)已知今年有150名学生报名学习大学先修课程,以前两年参加大学先修课程学习成绩的频率作为今年参加大学先修课程学习成绩的概率.
①在今年参与大学先修课程的学生中任取一人,求他获得某高校自主招生通过的概率;
②设今年全校参加大学先修课程的学生获得某高校自主招生通过的人数为![]() ,求
,求![]() .
.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
参考公式:![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表给出的是某城市![]() 年至
年至![]() 年,人均存款
年,人均存款![]() (万元),人均消费
(万元),人均消费![]() (万元)的几组对照数据.
(万元)的几组对照数据.
年份 |
|
|
|
|
人均存款 |
|
|
|
|
人均消费 |
|
|
|
|
(1)试建立![]() 关于
关于![]() 的线性回归方程;如果该城市
的线性回归方程;如果该城市![]() 年的人均存款为
年的人均存款为![]() 万元,请根据线性回归方程预测
万元,请根据线性回归方程预测![]() 年该城市的人均消费;
年该城市的人均消费;
(2)计算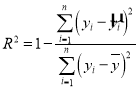 ,并说明线性回归方程的拟合效果.
,并说明线性回归方程的拟合效果.
附:回归方程![]() 中斜率和截距的最小二乘估计公式分别为
中斜率和截距的最小二乘估计公式分别为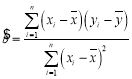 ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com