练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图，在四棱锥中，平面ABCD，，，，，E为PB的中点.

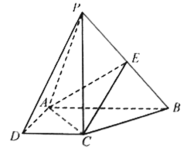
    （1）证明：平面平面PBC；

    （2）求直线PD与平面AEC所成角的正弦值.

    【答案】（1）证明见解析；（2）.

    【解析】

    （1）可先证明，，从而平面PBC，由此能证明平面平面PBC；

    （2）推导出,以C为原点，在平面ABCD中过C作CD的垂线为x轴，CD为y轴，CP为z轴，建立空间直角坐标系，利用向量法直线PD与平面AEC所成角的正弦值

    （1）证明：由平面ABCD，故.

    又，，，

    所以.

    故，.

    又，所以平面PBC，又平面

    所以平面平面PBC.

    （2）平面ABCD，故.

    又，.

    如图建立坐标系，

    ，，，，，.

    ∴， ， .

    设平面ACE的一个法量为，

    由，得，取，则

    故，

    设直线PD与平面AEC所成角为，

    则.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】在四棱锥中，，.

    (Ⅰ)若点为的中点，求证：∥平面；

    (Ⅱ)当平面平面时，求二面角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某工厂有甲、乙两生产车间，其污水瞬时排放量（单位：）关于时间（单位：）的关系均近似地满足函数，其图象如图所示：

    （1）根据图象求函数解析式；

    （2）若甲车间先投产，1小时后乙车间再投产，求该厂两车间都投产时刻的污水排放量；

    （3）由于受工厂污水处理能力的影响，环保部门要求该厂两车间任意时刻的污水排放量之和不超过，若甲车间先投产，为满足环保要求，乙车间比甲车间至少需推迟多少小时投产？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（1）当时，求证：；

    （2）求的单调区间；

    （3）设数列的通项,证明．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】一幅标准的三角板如图（1）中，为直角，，为直角，，且，把与拼齐使两块三角板不共面，连结如图（2）.

    （1）若是的中点，求证：；

    （2）在《九章算术》中，称四个面都是直角三角形的三棱锥为“鳖臑”，若图（2）中，三棱锥的体积为，则图（2）是否为鳖臑？说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】一个袋子里装有7个球，其中有红球4个.白球3个.这些球除颜色外全相同.

    （1）若一次从袋中取出3个球，取出的球颜色不完全相同的概率；

    （2）若一次从袋中取出3个球.其中若取到红球得0分，取到白球得1分，记随机变量为取出的三个小球得分之和，求的分布列，并求其数学期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知某超市为顾客提供四种结账方式：现金、支付宝、微信、银联卡.若顾客甲没有银联卡，顾客乙只带了现金，顾客丙、丁用哪种方式结账都可以，这四名顾客购物后，恰好用了其中的三种结账方式，那么他们结账方式的可能情况有（ ）种

    A. 19B. 7C. 26D. 12

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数的图象的一个对称中心与它相邻的一条对称轴之间的距离为．

    （1）求函数f（x）的对称轴方程及单调递增区间；

    （2）将函数y=f（x）的图象向右平移个单位后，再将得到的图象上所有点的横坐标缩短到原来的（纵坐标不变），得到函数y=g（x）的图象，当x∈（，）时，求函数g（x）的值域．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，若函数恰有7个不同零点,则实数a的取值范围是（ ）

    A.(0,1)B.[-1,1]C.(-1,1)D.(-1,0)∪(0,1)

    查看答案和解析>>

    同步练习册答案