练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知定义域为的函数同时满足以下三个条件：

    [1] 对任意的，总有；

    [2] ；

    [3] 若，，且，则有成立，

    并且称为“友谊函数”，请解答下列各题：

    (1)若已知为“友谊函数”，求的值；

    (2)函数在区间上是否为“友谊函数”？并给出理由.

    (3)已知为“友谊函数”，假定存在，使得且，

    求证：.

    （1）（2）为友谊函数


    解析:

    （1）取得，-------2分

    又由，得           --------------- 3分

    （2）显然在上满足[1] ；[2] .-------5分

    若，，且，则有

          故满足条件[1]、[2]、[3]，所以为友谊函数.--8分

    (3)由 [3]知任给其中，且有，不妨设则必有：-----------------------------9分

    所以：

    所以：.-----------------------------------10分

    依题意必有,

    下面用反证法证明：假设，则有或

    （1）若，则，这与矛盾；--12分

    (2)若，则，这与矛盾；

         故由上述（1）、（2）证明知假设不成立，则必有，证毕.----14分

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    定义：已知函数f（x）与g（x），若存在一条直线y=kx+b，使得对公共定义域内的任意实数均满足g（x）≤f（x）≤kx+b恒成立，其中等号在公共点处成立，则称直线y=kx+b为曲线f（x）与g（x）的“左同旁切线”．已知f（x）=Inx，g（x）=1-
    1
    x

    （I）证明：直线y=x-l是f（x）与g（x）的“左同旁切线”；
    （Ⅱ）设P（x1，f（x1）），Q（x2，f（x2））是函数 f（x）图象上任意两点，且0＜x1＜x2，若存在实数x3＞0，使得f′（x3）=
    f(x2)-f(x1)
    x2-x1
    ．请结合（I）中的结论证明x1＜x3＜x2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    若函数f（x）的定义域与值域都为同一区间D，则称函数f（x）为区间D上的“同势”函数．已知函数f（x）=x2-2x+1是区间D上的“同势”函数，则此区间可以是
    [0，
    3+
    		5
    2
    ]或[0，1]或[
    3+
    		5
    2
    ，+∞)等
    [0，
    3+
    		5
    2
    ]或[0，1]或[
    3+
    		5
    2
    ，+∞)等
    ．（只要写出一个你认为正确的区间即可）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    定义：已知函数f（x）与g（x），若存在一条直线y=kx+b，使得对公共定义域内的任意实数均满足f（x）≤g（x）≤kx+b恒成立，其中等号在公共点处成立，则称直线y=kx+b为曲线f（x）与g（x）的“左同旁切线”．已知f（x）=lnx，g（x）=1-
    1
    x
    ．
    （1）试探求f（x）与g（x）是否存在“左同旁切线”，若存在，请求出左同旁切线方程；若不存在，请说明理由．
    （2）设P（x1，f（x1）），Q（x2，f（x2））是函数f（x）图象上任意两点，0＜x1＜x2，且存在实数x3＞0，使得f（x3）=
    f(x2)-f(x1)
    x2-x1
    ，证明：x1＜x3＜x2．

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年河南省豫东、豫北十所名校高三测试理科数学试卷（解析版） 题型：解答题

    定义：已知函数f（x）与g（x），若存在一条直线y=kx +b，使得对公共定义域内的任意实数均满足g（x）≤f（x）≤kx+b恒成立，其中等号在公共点处成立，则称直线y=kx +b为曲线f（x）与g（x）的“左同旁切线”．已知

        （I）证明：直线y=x-l是f（x）与g（x）的“左同旁切线”；

        （Ⅱ）设P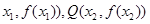（是函数 f（x）图象上任意两点，且0<x1<x2，若存在实数x3>0，使得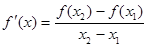．请结合（I）中的结论证明：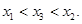

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    定义：已知函数f（x）与g（x），若存在一条直线y=kx+b，使得对公共定义域内的任意实数均满足g（x）≤f（x）≤kx+b恒成立，其中等号在公共点处成立，则称直线y=kx+b为曲线f（x）与g（x）的“左同旁切线”．已知f（x）=Inx，g（x）=1-数学公式
    （I）证明：直线y=x-l是f（x）与g（x）的“左同旁切线”；
    （Ⅱ）设P（x1，f（x1）），Q（x2，f（x2））是函数 f（x）图象上任意两点，且0＜x1＜x2，若存在实数x3＞0，使得f′（x3）=数学公式．请结合（I）中的结论证明x1＜x3＜x2．

    查看答案和解析>>

    同步练习册答案