
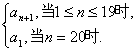 确定.记M=
确定.记M=(1)当k=1时,求M的值;
(2)求M的最小值及相应的k的值.
(文)设数列{an}的首项a1=a(a∈R),且an+1=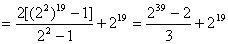 n=1,2,3,….
n=1,2,3,….
(1)若0<a<1,求a2、a3、a4、a5;
(2)若0<an<4,证明0<an+1<4;
(3)若0<a≤2,求所有的正整数k,使得对于任意n∈N*,均有an+k=an成立.
答案:(理)解:(1)显然an=2n-1,其中1≤n≤20.
当k=1时,bn=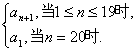 .
.
所以,![]()
![]() .
.
(2)M=![]()
![]()
![]() =
=![]() (40-k-2k)+
(40-k-2k)+![]() (220+k-220-k)
(220+k-220-k)
=![]() .
.
当2k=![]() ,即k=10时,M=
,即k=10时,M=![]() .
.
所以M的最小值为![]() ,此时k=10.
,此时k=10.
(文)(1)解:因为a1=a∈(0,1),所以a2=-a1+4=-a+4,且a2∈(3,4).所以a3=a2-3=-a+1,且a3∈(0,1).所以a4=-a3+4=a+3,且a4∈(3,4).所以a5=a4-3=a.
(2)证明:①当0<an≤3时,an+1=-an+4,所以1≤an+1<4.
②当3<an<4时,an+1=an-3,所以0<an+1<1.综上,0<an<4时,0<an+1<4.
(3)解:①若0<a<1,由(1),知a5=a1,所以k=4;因此,当k=4m(m∈N*)时,对所有的n∈N*,an+k=an成立.
②若1≤a<2,则a2=-a+4,且a2∈(2,3],a3=-a2+4=-(-a+4)+4=a=a1,所以k=2;因此,当k=2m(m∈N*)时,对所有的n∈N*,an+k=an成立.
③若a=2,则a2=a3=a4=…,所以k=1.因此,当k=m(m∈N*)时,对所有的n∈N*,an+k=an成立.
综上,若0<a<1,则k=4m;若1≤a<2,则k=2m;若a=2,则k=m(m∈N*).


科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(07年陕西卷理)
设集合S={A0,A1,A2,A3},在S上定义运算为:Ai![]() Aj=Ak,其中k为I+j被4除的余数,i、j=0,1,2,3.满足关系式=(x
Aj=Ak,其中k为I+j被4除的余数,i、j=0,1,2,3.满足关系式=(x![]() x)
x)![]() A2=A0的x(x∈S)的个数为
A2=A0的x(x∈S)的个数为
A.4 B.3 C.2 D.1
查看答案和解析>>
科目:高中数学 来源: 题型:
(04年浙江卷理)如图,△OBC的三个顶点坐标分别为(0,0)、(1,0)、(0,2),设P1为线段BC的中点,P2为线段CO的中点,P3为线段OP1的中点,对于每一个正整数n,Pn+3为线段PnPn+1的中点,令Pn的坐标为(xn,yn),an=![]() yn+yn+1+yn+2.
yn+yn+1+yn+2.
(1)求a1,a2,a3及an;
(2)证明![]() ,nÎN*;
,nÎN*;
(3)若记bn=y4n+4-y4n,nÎN*,证明{bn}是等比数列。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com