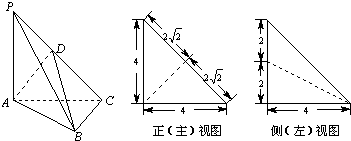
分析:(1)判断三角形ABC的形状,确定三棱锥P-ABC的外接球的半径,然后求解表面积;
(2)连接OC、OP,证明OC⊥AB,PO⊥AB,然后证明PO⊥OC,通过PO⊥AB,AB∩OC=O,说明PO⊥平面ABC.即可证明平面PAB⊥平面ABC;
(3)利用(2)的结果,确定棱锥的高,求出底面面积,即可求三棱锥P-ABC的体积.
解答:
解:(1)三棱锥P-ABC中,△PAC和△PBC是边长为
的等边三角形,AB=2,O是AB中点.
所以△ABC是直角三角形,∴OA=OB=OC=OP=1,
三棱锥P-ABC的外接球的半径r=1
∴表面积s=4π
(2)证明:连接OC、OP
∵AC=CB=
,O是AB中点,AB=2,∴OC⊥AB,OC=1.
同理,PO⊥AB,PO=1.
又PC=
,∴PC
2=OC
2+PO
2=2,
∴∠POC=90°,∴PO⊥OC.
∵PO⊥OC,PO⊥AB,AB∩OC=O,∴PO⊥平面ABC.
∵PO?平面PAB,∴平面PAB⊥平面ABC.
(3)由(2)可知PO⊥平面ABC,PO是棱锥的高,底面三角形ABC是直角三角形,
所以
v=×
AB•OC•OP=
××2×1×1=
.
点评:本题考查平面与平面存在的判断,棱锥的外接球的表面积的求法,棱锥的体积,考查空间想象能力计算能力.

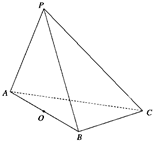 在三棱锥P-ABC中,△PAC和△PBC是边长为
在三棱锥P-ABC中,△PAC和△PBC是边长为 解:(1)三棱锥P-ABC中,△PAC和△PBC是边长为
解:(1)三棱锥P-ABC中,△PAC和△PBC是边长为

 提分百分百检测卷系列答案
提分百分百检测卷系列答案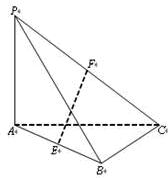 在三棱锥P-ABC中,PA⊥平面ABC.
在三棱锥P-ABC中,PA⊥平面ABC.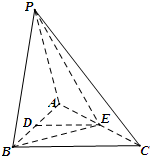 (2013•蚌埠二模)如图,在三棱锥P-ABC中,PA=PB=AB=2,BC=3,∠ABC=90°,平面PAB⊥平面ABC,D,E分别为AB,AC中点.
(2013•蚌埠二模)如图,在三棱锥P-ABC中,PA=PB=AB=2,BC=3,∠ABC=90°,平面PAB⊥平面ABC,D,E分别为AB,AC中点.