
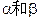 为平面,
为平面,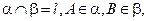 AB=5,A,B在棱l上的射影分别为A′,B′,AA′=3,BB′=2.若二面角
AB=5,A,B在棱l上的射影分别为A′,B′,AA′=3,BB′=2.若二面角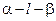 的大小为
的大小为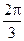 ,求:
,求: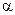 的距离;
的距离;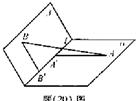
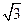
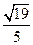
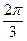 .因此在Rt△BB′D中,BB′=2,∠BB′D=π-∠BB′C=
.因此在Rt△BB′D中,BB′=2,∠BB′D=π-∠BB′C=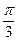 ,BD=BB′·sinBB′D=
,BD=BB′·sinBB′D=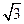 .
.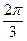 ,则由余弦定理,
,则由余弦定理,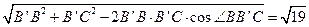 .
. 平面
平面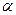 ,且DC
,且DC CA,由三垂线定理知AC
CA,由三垂线定理知AC BC.
BC.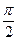 ,sinBAC=
,sinBAC=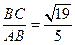 .
.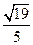


科目:高中数学 来源:不详 题型:解答题
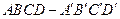 中,AP=BQ=b(0<b<1),截面PQEF∥
中,AP=BQ=b(0<b<1),截面PQEF∥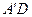 ,截面PQGH∥
,截面PQGH∥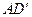 .
.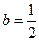 ,求
,求 与平面PQEF所成角的正弦值.
与平面PQEF所成角的正弦值.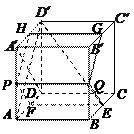
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
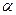 内作菱形ABCD,边长为1,∠BAD=60°,再在
内作菱形ABCD,边长为1,∠BAD=60°,再在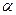 的上方,分别以△
的上方,分别以△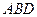 与△
与△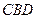 为底面安装上相同的正棱锥P-ABD与Q-CBD,∠APB=90°.
为底面安装上相同的正棱锥P-ABD与Q-CBD,∠APB=90°.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
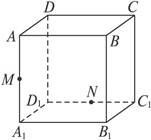
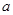 升水时,水面恰好经过正四棱锥的顶点P。如果将容器倒置,水面也恰好过点
升水时,水面恰好经过正四棱锥的顶点P。如果将容器倒置,水面也恰好过点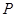 (图2)。有下列四个命题:
(图2)。有下列四个命题:| A.正四棱锥的高等于正四棱柱高的一半 |
B.将容器侧面水平放置时,水面也恰好过点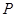 |
C.任意摆放该容器,当水面静止时,水面都恰好经过点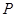 |
D.若往容器内再注入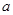 升水,则容器恰好能装满 升水,则容器恰好能装满 |

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com