
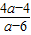 =
=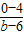 ,解得 b 的值,求得B的坐标为(
,解得 b 的值,求得B的坐标为(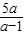 ,0),根据△OAB面积为 S=
,0),根据△OAB面积为 S=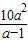 ,即10a2-Sa+S=0,利用判别式大于或等于零求出S的最小值,并求出此时a的值 即可得到B的坐标.
,即10a2-Sa+S=0,利用判别式大于或等于零求出S的最小值,并求出此时a的值 即可得到B的坐标.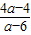 =
=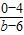 ,解得 b=
,解得 b=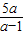 ,
,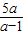 ,0),故△OAB面积为 S=
,0),故△OAB面积为 S=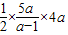 =
=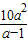 ,即 10a2-Sa+S=0.
,即 10a2-Sa+S=0.

 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
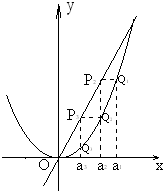 (2013•广州三模)如图,已知直线l:y=4x及曲线C:y=x2,C上的点Q1的横坐标为a1(0<a1<4).从曲线C上的点Qn(n≥1)作直线平行于x轴,交直线l于点Pn+1,再从点Pn+1作直线平行于y轴,交曲线C于点Qn+1.Qn(n=1,2,3,…)的横坐标构成数列{an}.
(2013•广州三模)如图,已知直线l:y=4x及曲线C:y=x2,C上的点Q1的横坐标为a1(0<a1<4).从曲线C上的点Qn(n≥1)作直线平行于x轴,交直线l于点Pn+1,再从点Pn+1作直线平行于y轴,交曲线C于点Qn+1.Qn(n=1,2,3,…)的横坐标构成数列{an}.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com