
| 1 |
| 2 |
| 4 |
| 5 |
| 1 |
| 10 |
| 3 |
| 7 |
| x+a-1 |
| x+2a |
| a+1 |
| x+2a |
| 1 |
| 2 |
| 4 |
| 5 |
|
| x |
| x+2 |
| an |
| an+2 |
| 1 |
| an+1 |
| 1 |
| an |
| 1 |
| an |
| 1 |
| 2n-1 |
| 1 |
| (2n-1)•(2n+1-1) |
| 1 |
| 3 |
| 3 |
| 7 |
| 1 |
| 3 |
| 1 |
| 21 |
| 16 |
| 42 |
| 3 |
| 7 |
| anan+1 |
| an-1an |
| 2n-1-1 |
| 2n+1-2 |
| 1 |
| 2 |
| 2n-1-1 |
| 2n-1 |
| 1 |
| 2 |
| 3 |
| 7 |
| x+a-1 |
| x+2a |
| a+1 |
| x+2a |
| 1 |
| 2 |
| 4 |
| 5 |
|
|
|
| x |
| x+2 |
| an |
| an+2 |
| 1 |
| an+1 |
| 1 |
| an |
| 1 |
| an+1 |
| 1 |
| an |
| 1 |
| an |
| bn+1 |
| bn |
| b2 |
| b1 |
| b3 |
| b2 |
| bn |
| bn-1 |
| ||
| n¡— |
| 1 |
| an |
| 1 |
| 2n-1 |
| 1 |
| 10 |
| 1 |
| 2n-1 |
| 1 |
| 10 |
| 1 |
| 2n-1 |
| 1 |
| (2n-1)•(2n+1-1) |
| 1 |
| 3 |
| 3 |
| 7 |
| 1 |
| 3 |
| 1 |
| 21 |
| 16 |
| 42 |
| 3 |
| 7 |
| anan+1 |
| an-1an |
| 2n-1-1 |
| 2n+1-1 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 21 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 21 |
| 1 |
| 20 |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 2n-2 |
| 1 |
| 3 |
| 2 |
| 21 |
| 1 |
| 2n-1 |
| 1 |
| 3 |
| 2 |
| 21 |
| 18 |
| 42 |
| 3 |
| 7 |


 ç¥îÏÆŠýãòåüçêÅÇÞ¯¡
ç¥îÏÆŠýãòåüçêÅÇÞ¯¡ Åôñúñý§ä¡´°ÍÇä100ñøüçêÅÇÞ¯¡
Åôñúñý§ä¡´°ÍÇä100ñøüçêÅÇÞ¯¡
| áõ¥Ñ | ¡ÔøÅ¢ö°ä | áõ¥Ñ | °¾øÅ¢ö°ä |
| ¡ÔØ£ | ¡ÔØ£ûãñî¢ö°äëó¥—ÈÀ | °¾Ø£ | °¾Ø£ûãñî¢ö°äëó¥—ÈÀ |
| ¡Ôѱ | ¡Ôѱûãñî¢ö°äëó¥—ÈÀ | °¾Ñ± | °¾Ñ±ûãñî¢ö°äëó¥—ÈÀ |
| ¡Ôà» | ¡Ôà»ûãñî¢ö°äëó¥—ÈÀ | °¾à» | °¾à»ûãñî¢ö°äëó¥—ÈÀ |
¢óá¢È¤¡ÔøÅò»îÏ âÇåÇȤ äãÅëȤ
| 2 | f(x) |
ýÕ¢ÇÇÞ¯¡¤ë§ãö—>>
¢óá¢È¤¡ÔøÅò»îÏ âÇåÇȤ äãÅëȤ
| 1 |
| 2 |
| 4 |
| 5 |
| 1 |
| 10 |
ýÕ¢ÇÇÞ¯¡¤ë§ãö—>>
¢óá¢È¤¡ÔøÅò»îÏ âÇåÇȤ äãÅëȤ§ãÇÞäã
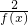 åÖMáÖöˆå—¤₤ò»ÈÛ
åÖMáÖöˆå—¤₤ò»ÈÛýÕ¢ÇÇÞ¯¡¤ë§ãö—>>
¢óá¢È¤¡ÔøÅò»îÏ âÇåÇȤ2009-2010îÏáõùáÇ´òÀáü°ðØ£øÅ¡Ôà»È´üôÈˋ6åôòòÆÎÅ墥òåò»îÏòåƒÚÈ´âÚ¢óÈˋÈ´§ãö—¯ÌÈˋ äãÅëȤ§ãÇÞäã
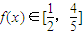 òÝȘúµxçáàÀøçñÑöÏÈ£
òÝȘúµxçáàÀøçñÑöÏÈ£ ¤Ð°èêÂȘúµæŸÅÀçáNÈ£
¤Ð°èêÂȘúµæŸÅÀçáNÈ£ ÈÛ
ÈÛýÕ¢ÇÇÞ¯¡¤ë§ãö—>>
¯ìÑàøôÅé - êñü¯ýÃêÅÝÚ - òåäãêÅÝÚ
¤±ÝÝòÀ£Ëêˆë½öËñ´¤ëý£ê¥ÅéüƒìÝ´ó§ä´ | ë½èüÆŤÎÅéüƒìÝ´æ´ú½ | çÓÅéíˋóÙƒìÝ´æ´ú½ | èÌâºòñÅÕößø¼ØÍÆŤÎÅéüƒìÝ´æ´ú½ | èÌóµúøà´ƒìÝ´æ´ú½
öËñ´¤ëý£ê¥ÅéüƒìÝ´çÓ£¯È¤027-86699610 ƒìÝ´ÆòüðȤ58377363@163.com