
【题目】已知点![]() 是抛物线
是抛物线![]() 的焦点,
的焦点,![]() 是抛物线
是抛物线![]() 在第一象限内的点,且
在第一象限内的点,且![]() ,
,
(I) 求![]() 点的坐标;
点的坐标;
(II)以![]() 为圆心的动圆与
为圆心的动圆与![]() 轴分别交于两点
轴分别交于两点![]() ,延长
,延长![]() 分别交抛物线
分别交抛物线![]() 于
于![]() 两点;
两点;
①求直线![]() 的斜率;
的斜率;
②延长![]() 交
交![]() 轴于点
轴于点![]() ,若
,若![]() ,求
,求![]() 的值.
的值.
【答案】(I)![]() (II)①
(II)①![]() ②
②![]()
【解析】
(I)由抛物线的定义,可求出![]() 点的横坐标,代入方程中,求出
点的横坐标,代入方程中,求出![]() 点的纵坐标;
点的纵坐标;
(II) ①设直线SA的斜率为k,可设出SA直线方程,与抛物线方程联立,求出点M的坐标,由题意可知:SA=SB,因此可求出直线SB的斜率,可设出直线SB的方程,同理,可以求出N点的坐标,代入斜率公式,求出直线![]() 的斜率;
的斜率;
②设出E点坐标,由![]() ,可得到
,可得到![]() ,从而求出斜率k,求出A点坐标,同理求出B点坐标,利用余弦定理求出
,从而求出斜率k,求出A点坐标,同理求出B点坐标,利用余弦定理求出![]() 的值,也就求出
的值,也就求出![]() 的值。
的值。
如下图所示:
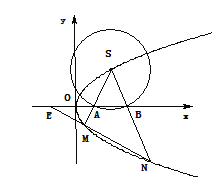
(I)设![]() ,抛物线的焦点为
,抛物线的焦点为![]() ,准线方程为
,准线方程为![]() 由抛物线的定义可知
由抛物线的定义可知![]() ,所以
,所以![]() 点的坐标为(1,1);
点的坐标为(1,1);
(II) ①设直线SA的直线方程为:![]() 与抛物线方程联立:
与抛物线方程联立:
![]() ,设
,设![]() ,
,![]() ,
,
所以![]() ,因为以
,因为以![]() 为圆心的动圆与
为圆心的动圆与![]() 轴分别交于两点
轴分别交于两点![]() ,所以SA=SB,因此直线SB的斜率为-k,同理可求出
,所以SA=SB,因此直线SB的斜率为-k,同理可求出![]() ,
,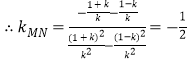 ;
;
②设![]() ,
,![]()
![]() ,
,
![]() ,
,
则直线SA的方程为![]() ,A点坐标为
,A点坐标为![]() ,同理B点坐标为
,同理B点坐标为![]() ,
,![]() ,
,
![]() ,所以
,所以![]()


科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是边长为2的正方形,平面
是边长为2的正方形,平面![]()
![]()
![]() 为等腰直角三角形,
为等腰直角三角形,![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 的中点.
的中点.
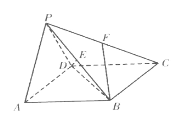
(1)求异面直线![]() 与
与![]() 所成角的余弦值;
所成角的余弦值;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】抢“微信红包”已经成为中国百姓欢度春节时非常喜爱的一项活动.小明收集班内20名同学今年春节期间抢到红包金额![]() (元)如下(四舍五入取整数):
(元)如下(四舍五入取整数):
102 52 41 121 72
162 50 22 158 46
43 136 95 192 59
99 22 68 98 79
对这20个数据进行分组,各组的频数如下:
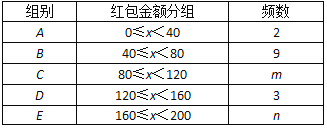
(Ⅰ)写出m,n的值,并回答这20名同学抢到的红包金额的中位数落在哪个组别;
(Ⅱ)记C组红包金额的平均数与方差分别为![]() 、
、![]() ,E组红包金额的平均数与方差分别为
,E组红包金额的平均数与方差分别为![]() 、
、![]() ,试分别比较
,试分别比较![]() 与
与![]() 、
、![]() 与
与![]() 的大小;(只需写出结论)
的大小;(只需写出结论)
(Ⅲ)从A,E两组所有数据中任取2个,求这2个数据差的绝对值大于100的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】研究发现,北京 PM 2.5 的重要来源有土壤尘、燃煤、生物质燃烧、汽车尾气与垃圾焚烧、工业污染和二次无机气溶胶,其中燃煤的平均贡献占比约为 18%.为实现“节能减排”,还人民“碧水蓝天”,北京市推行“煤改电”工程,采用空气源热泵作为冬天供暖.进入冬季以来,该市居民用电量逐渐增加,为保证居民取暖,市供电部门对该市 100 户居民冬季(按 120 天计算)取暖用电量(单位:度)进行统计分析,得到居民冬季取暖用电量的频率分布直方图如图所示.

(1)求频率分布直方图中![]() 的值;
的值;
(2)从这 100 户居民中随机抽取 1 户进行深度调查,求这户居民冬季取暖用电量在[3300,3400]的概率;
(3)在用电量为[3200,3250),[3250,3300),[3300,3350),[3350,3400]的四组居民中,用分层抽样的方法抽取 34 户居民进行调查,则应从用电量在[3200,3250)的居民中抽取多少户?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是60名学生参加数学竞赛的成绩(均为整数)的频率分布直方图,估计这次数学竞赛的及格率(60分及以上为及格)是( )

A. 0.9 B. 0.75 C. 0.8 D. 0.7
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分16分)
已知数列{an}的前n项和为Sn,且a1=1,Sn=n2an(n∈N*).
(1)试求出S1,S2,S3,S4,并猜想Sn的表达式;
(2)用数学纳法证明你的猜想,并求出an的表达式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
如图,在直四棱柱ABCD-A![]() B
B![]() C
C![]() D
D![]() 中,底面ABCD为等腰梯形,AB//CD,AB=4,BC=CD=2,AA
中,底面ABCD为等腰梯形,AB//CD,AB=4,BC=CD=2,AA![]() =2,E、E
=2,E、E![]() 分别是棱AD、AA
分别是棱AD、AA![]() 的中点.
的中点.

(1)设F是棱AB的中点,证明:直线EE![]() //平面FCC
//平面FCC![]() ;
;
(2)证明:平面D1AC⊥平面BB1C1C.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在多面体ABCDEF中,ABCD是正方形,BF⊥平面ABCD,DE⊥平面ABCD,BF=DE,点M为棱AE的中点.
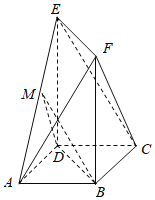
(1)求证:平面BMD∥平面EFC;
(2)若AB=1,BF=2,求三棱锥A-CEF的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com