
【题目】已知f(x)为定义在[﹣1,1]上的奇函数,当x∈[﹣1,0]时,函数解析式为 ![]() .
.
(Ⅰ)求f(x)在[0,1]上的解析式;
(Ⅱ)求f(x)在[0,1]上的最值.
【答案】解:(Ⅰ)设x∈[0,1],则﹣x∈[﹣1,0].∴f(x)= ![]() =4x﹣2x又∵f(﹣x)=﹣f(x)=﹣(4x﹣2x)∴f(x)=2x﹣4x .
=4x﹣2x又∵f(﹣x)=﹣f(x)=﹣(4x﹣2x)∴f(x)=2x﹣4x .
所以,f(x)在[0,1]上的解析式为f(x)=2x﹣4x
(Ⅱ)当x∈[0,1],f(x)=2x﹣4x=﹣(2x)2+2x ,
∴设t=2x(t>0),则y=﹣t2+t∵x∈[0,1],∴t∈[1,2]
当t=1时x=0,f(x)max=0;当t=2时x=1,f(x)min=﹣2
【解析】(Ⅰ)设x∈[0,1],则﹣x∈[﹣1,0],利用条件结合奇函数的定义求f(x)在[0,1]上的解析式;(Ⅱ)设t=2x(t>0),则y=﹣t2+t,利用二次函数的性质求f(x)在[0,1]上的最值.


科目:高中数学 来源: 题型:
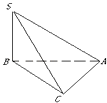
【题目】三棱锥S﹣ABC中,∠SBA=∠SCA=90°,△ABC是斜边AB=a的等腰直角三角形,则以下结论中: ①异面直线SB与AC所成的角为90°;
②直线SB⊥平面ABC;
③面SBC⊥面SAC;
④点C到平面SAB的距离是 ![]() .
.
其中正确结论的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等比数列{an}中a2=2,a5= ![]() ,则a1a2+a2a3+a3a4+…+anan+1等于( )
,则a1a2+a2a3+a3a4+…+anan+1等于( )
A.16(1﹣4﹣n)
B.16(1﹣2n)
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=3x2﹣kx﹣8,x∈[1,5].
(1)当k=12时,求f(x)的值域;
(2)若函数f(x)具有单调性,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图示:半圆O的直径为2,A为直径延长线上的一点,OA=2,B为半圆上任意一
点,以AB为一边作等边三角形ABC.则四边形OACB的面积最大值是 . 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设离心率为 ![]() 的椭圆
的椭圆![]() 的左、右焦点为
的左、右焦点为![]() , 点P是E上一点,
, 点P是E上一点, ![]() ,
, ![]() 内切圆的半径为
内切圆的半径为 ![]() .
.
(1)求E的方程;
(2)矩形ABCD的两顶点C、D在直线![]() 上,A、B在椭圆E上,若矩形ABCD的周长为
上,A、B在椭圆E上,若矩形ABCD的周长为 ![]() , 求直线AB的方程.
, 求直线AB的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,a,b,c分别是角A,B,C的对边,且2cosAcosC(1-tanAtanC)=1.
(1)求B的大小;
(2)若b=![]() ,求△ABC面积的最大值.
,求△ABC面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】脱贫是政府关注民生的重要任务,了解居民的实际收入状况就显得尤为重要.现从某地区随机抽取100个农户,考察每个农户的年收入与年积蓄的情况进行分析,设第i个农户的年收入xi(万元),年积蓄yi(万元),经过数据处理得 ![]() . (Ⅰ)已知家庭的年结余y对年收入x具有线性相关关系,求线性回归方程;
. (Ⅰ)已知家庭的年结余y对年收入x具有线性相关关系,求线性回归方程;
(Ⅱ)若该地区的农户年积蓄在5万以上,即称该农户已达小康生活,请预测农户达到小康生活的最低年收入应为多少万元?
附:在 ![]() =
= ![]() x+
x+ ![]() 中,
中, ![]() =
=  ,
, ![]() =
= ![]() ﹣
﹣ ![]() ,其中
,其中 ![]() 为样本平均值.
为样本平均值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com