
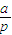 [(1+p)4-(1+p)]
[(1+p)4-(1+p)]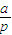 [(1+p)5-(1+p)]
[(1+p)5-(1+p)]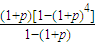 =
=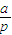 [(1+p)5-(1+p)].
[(1+p)5-(1+p)].

 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源: 题型:
| A、a(1+p)4 | ||
| B、a(1+p)5 | ||
C、
| ||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、m(1+r)6 | ||
| B、m(1+r)7 | ||
C、
| ||
D、
|
查看答案和解析>>
科目:高中数学 来源:2010年江西省高三热身卷数学(理)试题 题型:选择题
某人为了观看2010年南非世界杯,2004年起,每年5月10日到银行存入m元定期储蓄,若年利率为r且保持不变,并约定每年到期存款均自动转为新的一年定期,到2010年5月10日将所有存款和利息全部取回,则可取回钱的总数(元)为( )
A.m(1+r)6 B.m(1+r)7
C.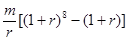 D.
D.
查看答案和解析>>
科目:高中数学 来源:2011年高考数学复习:5.5 数列的综合应用(解析版) 题型:选择题
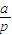 [(1+p)4-(1+p)]
[(1+p)4-(1+p)]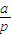 [(1+p)5-(1+p)]
[(1+p)5-(1+p)]查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com