练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】某地通过市场调查得到西红柿种植成本（单位：元/千克）与上市时间（单位：天）的数据如下表：

    时间

    种植成本

    （1）根据上表数据，发现二次函数能够比较准确描述与的变化关系，请求出函数的解析式；

    （2）利用选取的函数，求西红柿最低种植成本及此时的上市天数.

    【答案】（1）Qt2﹣4t．（2）西红柿种植成本Q最低为（元/kg）

    【解析】

    （1）由待定系数法求解析式即可

    （2）配方利用二次函数求最值

    (1)根据题意,设西红柿种植成本Q与上市时间t的函数关系为Q，

    把表格提供的三对数据代入该解析式得到：解得a，b＝﹣4，c．

    所以，西红柿种植成本Q与上市时间t的函数关系是Qt2﹣4t．

    （2）Qt2﹣4t（t﹣3）2

    当t＝3，即在第150天时，西红柿种植成本Q最低为（元/kg）

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，在正方体中，，分别是棱，的中点，为棱上一点，且平面.

    （1）证明：为中点；

    （2）求平面与平面所成锐二面角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为了解学生的课外阅读时间情况，某学校随机抽取了 50人进行统计分析，把这50人每天阅读的时间(单位:分钟)绘制成频数分布表，如下表所示：

    若把每天阅读时间在60分钟以上（含60分钟）的同学称为“阅读达人”，根据统计结果中男女生阅读达人的数据，制作出如图所示的等高条形图.

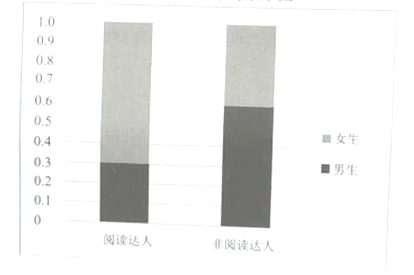
    （1）根据抽样结果估计该校学生的每天平均阅读时间（同一组数据用该区间的中点值作为代表）；

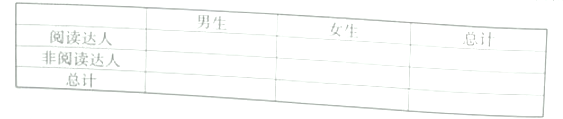
    （2）根据已知条件完成下面的列联表，并判断是否有的把握认为“阅读达人”跟性别有关？

    附：参考公式

    ，其中.

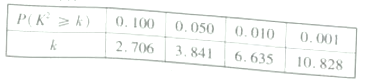
    临界值表：

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数．

    （1）已知f（x）的图象关于原点对称，求实数的值；

    （2）若，已知常数满足：对任意恒成立，求实数的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数是定义域在上的奇函数，且．

    （1）用定义证明：函数在上是增函数，

    （2）若实数满足，求实数的范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知直线l：mx﹣y＝1，若直线l与直线x+m（m﹣1）y＝2垂直，则m的值为_____，动直线l：mx﹣y＝1被圆C：x2﹣2x+y2﹣8＝0截得的最短弦长为_____．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设E，F分别是正方体ABCD﹣A1B1C1D1的棱DC上两点，且AB＝2，EF＝1，给出下列四个命题：

    ①三棱锥D1﹣B1EF的体积为定值；

    ②异面直线D1B1与EF所成的角为45°；

    ③D1B1⊥平面B1EF；

    ④直线D1B1与平面B1EF所成的角为60°．

    其中正确的命题为_____．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=﹣alnx+（a+1）x﹣（a＞0）．

    （1）讨论函数f（x）的单调性；

    （2）若f（x）≥﹣+ax+b恒成立，求a时，实数b的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，.

    （1）求函数在点处的切线方程；

    （2）求函数的单调区间；

    （3） 求证：当时，恒成立.

    查看答案和解析>>

    同步练习册答案