
【题目】已知函数![]() .
.
(1)当![]() 时,比较
时,比较![]() 与1的大小;
与1的大小;
(2)当![]() 时,如果函数
时,如果函数![]() 仅有一个零点,求实数
仅有一个零点,求实数![]() 的取值范围;
的取值范围;
(3)求证:对于一切正整数![]() ,都有
,都有![]() .
.
【答案】(1)当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() ;(2)
;(2)![]() 或
或![]() ;(3)证明见解析.
;(3)证明见解析.
【解析】试题分析: (1)当![]() 时,
时, ![]() ,其定义域为
,其定义域为![]() ,令
,令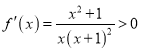
![]()
![]() 在
在![]() 上是增函数
上是增函数![]() 故当
故当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() ;(2)当
;(2)当![]() 时
时![]()
![]() ,其定义域为
,其定义域为![]() ,令
,令
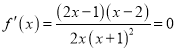
![]()
![]()
![]() 当
当![]() 或
或![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]()
![]() 函数
函数![]() 在
在![]() 上递增,在
上递增,在![]() 上递减,在
上递减,在![]() 上递增
上递增![]()
![]() 的极大值为
的极大值为![]() ,极小值为
,极小值为![]() ,又当
,又当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() ,
, ![]()
![]() 或
或![]() ;(3)根据(1)的结论知当
;(3)根据(1)的结论知当![]() 时,
时, ![]()
![]() 即当
即当![]() 时,
时, ![]()
![]()
![]() ,令
,令![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
所以![]() .
.
试题解析: (1)当![]() 时,
时, ![]() ,其定义域为
,其定义域为![]() ,因为
,因为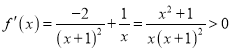 ,所以
,所以![]() 在
在![]() 上是增函数,
上是增函数,
故当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() ;
;
当![]() 时,
时, ![]()
(2)当![]() 时,
时, ![]() ,其定义域为
,其定义域为![]() ,
,
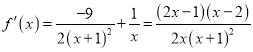 ,令
,令![]() 得
得![]() ,
,
因为当![]() 或
或![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() ,
,
所以函数![]() 在
在![]() 上递增,在
上递增,在![]() 上递减,在
上递减,在![]() 上递增且
上递增且![]() 的极大值为
的极大值为![]() ,极小值为
,极小值为![]() ,又当
,又当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() ,
,
因为函数![]() 仅有一个零点,所以函数
仅有一个零点,所以函数![]() 的图象与直线
的图象与直线![]() 仅有一个交点.所以
仅有一个交点.所以![]() 或
或![]() ;
;
(3)根据(1)的结论知当![]() 时,
时, ![]() .
.
即当![]() 时,
时, ![]() ,即
,即![]() 令
令![]() ,则有
,则有![]() ,
,
从而得![]() ,
,
故得![]() ,
,
即![]() ,
,
所以![]() .
.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)为二次函数,且f(x﹣1)+f(x)=2x2+4.
(1)求f(x)的解析式;
(2)当x∈[t,t+2],t∈R时,求函数f(x)的最小值(用t表示).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,将绘有函数f(x)=2sin(ωx+φ)(ω>0, ![]() <φ<π)部分图象的纸片沿x轴折成直二面角,若AB之间的空间距离为
<φ<π)部分图象的纸片沿x轴折成直二面角,若AB之间的空间距离为 ![]() ,则f(﹣1)=( )
,则f(﹣1)=( ) 
A.﹣2
B.2
C.- ![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a=log3650.99、b=1.01365、c=0.99365 , 则a、b、c的大小关系为( )
A.a<c<b
B.b<a<c
C.a<b<c
D.b<c<a
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某天连续有![]() 节课,其中语文、英语、物理、化学、生物
节课,其中语文、英语、物理、化学、生物![]() 科各
科各![]() 节,数学
节,数学![]() 节.在排课时,要求生物课不排第
节.在排课时,要求生物课不排第![]() 节,数学课要相邻,英语课与数学课不相邻,则不同排法的种数是( )
节,数学课要相邻,英语课与数学课不相邻,则不同排法的种数是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)=ax2+2x+c(a≠0),函数f(x)对于任意的都满足条件f(1+x)=f(1﹣x).
(1)若函数f(x)的图象与y轴交于点(0,2),求函数f(x)的解析式;
(2)若函数f(x)在区间(0,1)上有零点,求实数c的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,设椭圆![]() :
: ![]() 的离心率为
的离心率为![]() ,
, ![]() 分别为椭圆
分别为椭圆![]() 的左、右顶点,
的左、右顶点, ![]() 为右焦点,直线
为右焦点,直线![]() 与
与![]() 的交点到
的交点到![]() 轴的距离为
轴的距离为![]() ,过点
,过点![]() 作
作![]() 轴的垂线
轴的垂线![]() ,
, ![]() 为
为![]() 上异于点
上异于点![]() 的一点,以
的一点,以![]() 为直径作圆
为直径作圆![]() .
.
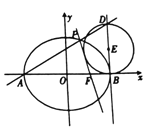
(1)求![]() 的方程;
的方程;
(2)若直线![]() 与
与![]() 的另一个交点为
的另一个交点为![]() ,证明:直线
,证明:直线![]() 与圆
与圆![]() 相切.
相切.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市公租房的房源位于A、B、C三个片区,设每位申请人只申请其中一个片区的房源,且申请其中任一个片区的房源是等可能的,求该市的任4位申请人中:
(1)恰有2人申请A片区房源的概率;
(2)申请的房源所在片区的个数的ξ分布列与期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com