
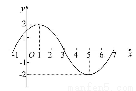
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<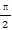 ,x∈R)的图象的一部分如图所示.
,x∈R)的图象的一部分如图所示.
(1)求函数f(x)的解析式.
(2)当x∈[-6,- ]时,求函数y=f(x)+f(x+2)的最大值与最小值及相应的x的值.
]时,求函数y=f(x)+f(x+2)的最大值与最小值及相应的x的值.
(1) f(x)=2sin( x+
x+ )
)
(2) 当 x=-
x=- ,即x=-
,即x=-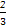 时,y=f(x)+f(x+2)取得最大值
时,y=f(x)+f(x+2)取得最大值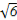 ;
;
当 x=-π,即x=-4时,y=f(x)+f(x+2)取得最小值-2
x=-π,即x=-4时,y=f(x)+f(x+2)取得最小值-2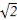 .
.
【解析】(1)由图象知A=2,T=8,
∵T=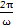 =8,∴ω=
=8,∴ω= .
.
又图象经过点(-1,0),∴2sin(- +φ)=0,
+φ)=0,
∴φ=kπ+ ,k∈Z,∵|φ|<
,k∈Z,∵|φ|< ,
,
∴φ= .∴f(x)=2sin(
.∴f(x)=2sin( x+
x+ ).
).
(2)y=f(x)+f(x+2)
=2sin( x+
x+ )+2sin(
)+2sin( x+
x+ +
+ )
)
=2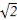 cos
cos x.
x.
∵x∈[-6,-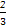 ],∴-
],∴-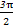 ≤
≤ x≤-
x≤- .
.
∴当 x=-
x=- ,即x=-
,即x=-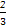 时,y=f(x)+f(x+2)取得最大值
时,y=f(x)+f(x+2)取得最大值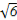 ;
;
当 x=-π,即x=-4时,y=f(x)+f(x+2)取得最小值-2
x=-π,即x=-4时,y=f(x)+f(x+2)取得最小值-2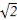 .
.


科目:高中数学 来源:2014年高考数学全程总复习课时提升作业五十二第八章第三节练习卷(解析版) 题型:选择题
过点A(11,2)作圆x2+y2+2x-4y-164=0的弦,其中弦长为整数的共有( )
(A)16条 (B)17条 (C)32条 (D)34条
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业五十七第八章第八节练习卷(解析版) 题型:填空题
设椭圆方程为x2+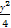 =1,过点M(0,1)的直线l交椭圆于A,B两点,O是坐标原点,点P满足
=1,过点M(0,1)的直线l交椭圆于A,B两点,O是坐标原点,点P满足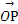 =
=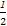 (
(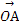 +
+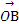 ),当l绕点M旋转时,动点P的轨迹方程为 .
),当l绕点M旋转时,动点P的轨迹方程为 .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业五十一第八章第二节练习卷(解析版) 题型:选择题
若动点A(x1,y1),B(x2,y2)分别在直线l1:x+y-7=0和l2:x+y-5=0上移动,则线段AB的中点M到原点的距离的最小值为( )
(A)2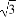 (B)3
(B)3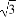 (C)3
(C)3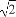 (D)4
(D)4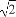
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业五十一第八章第二节练习卷(解析版) 题型:选择题
对任意实数a,直线y=ax-3a+2所经过的定点是( )
(A)(2,3) (B)(3,2)
(C)(-2,3) (D)(3,-2)
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业二十第三章第四节练习卷(解析版) 题型:填空题
已知函数y=Asin(ωx+φ)(A>0,ω>0,0<φ<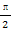 )的图象经过点(0,1),且
)的图象经过点(0,1),且 一个最高点的坐标为(1,2),则ω的最小值是 .
一个最高点的坐标为(1,2),则ω的最小值是 .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业二十四第三章第八节练习卷(解析版) 题型:解答题
如图,摄影爱好者在某公园A处,发现正前方B处有一立柱,测得立柱顶端O的仰角和立柱底部B的俯角均为30°,已知摄影爱好者的身高约为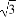 米(将眼睛S距地面的距离SA按
米(将眼睛S距地面的距离SA按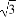 米处理).
米处理).
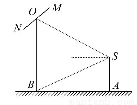
(1)求摄影爱好者到立柱的水平距离AB和立柱的高度OB.
(2)立柱的顶端有一长为2米的彩杆MN,且MN绕其中点O在摄影爱好者与立柱所在的平面内旋转.在彩杆转动的任意时刻,摄影爱好者观察彩杆MN的视角∠MSN(设为θ)是否存在最大值?若存在,请求出∠MSN取最大值时cosθ的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业二十六第四章第二节练习卷(解析版) 题型:填空题
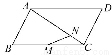
如图,在?ABCD中,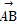 =a,
=a,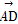 =b,
=b,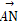 =3
=3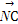 ,M是BC的中点,则
,M是BC的中点,则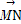 = (用a,b表示).
= (用a,b表示).
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业二十五第四章第一节练习卷(解析版) 题型:选择题
已知O是△ABC所在平面内一点,D为BC边中点,且2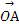 +
+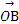 +
+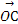 =0,那么( )
=0,那么( )
(A)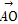 =
= (B)
(B)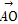 =2
=2
(C)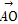 =3
=3 (D)2
(D)2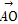 =
=
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com