
【题目】甲、乙两人同时参加一次数学测试,共有![]() 道选择题,每题均有
道选择题,每题均有![]() 个选项,答对得
个选项,答对得![]() 分,答错或不答得
分,答错或不答得![]() 分.甲和乙都解答了所有的试题,经比较,他们只有
分.甲和乙都解答了所有的试题,经比较,他们只有![]() 道题的选项不同,如果甲最终的得分为
道题的选项不同,如果甲最终的得分为![]() 分,那么乙的所有可能的得分值组成的集合为____________.
分,那么乙的所有可能的得分值组成的集合为____________.
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:高中数学 来源: 题型:
【题目】已知抛物线![]() (
(![]() )与双曲线
)与双曲线![]() (
(![]() ,
,![]() )有相同的焦点
)有相同的焦点![]() ,点
,点![]() 是两条曲线的一个交点,且
是两条曲线的一个交点,且![]() 轴,则该双曲线经过一、三象限的渐近线的倾斜角所在的区间是( )
轴,则该双曲线经过一、三象限的渐近线的倾斜角所在的区间是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有次水下考古活动中,潜水员需潜入水深为30米的水底进行作业,其用氧量包含以下三个方面:①下潜时,平均速度为每分钟![]() 米,每分钟的用氧量为
米,每分钟的用氧量为![]() 升;②水底作业需要10分钟,每分钟的用氧量为0.3升;③返回水面时,速度为每分钟
升;②水底作业需要10分钟,每分钟的用氧量为0.3升;③返回水面时,速度为每分钟![]() 米,每分钟用氧量为0.2升;设潜水员在此次考古活动中的总用氧量为
米,每分钟用氧量为0.2升;设潜水员在此次考古活动中的总用氧量为![]() 升;
升;
(1)将![]() 表示为
表示为![]() 的函数;
的函数;
(2)若![]() ,求总用氧量
,求总用氧量![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近来天气变化无常,陡然升温、降温幅度大于![]() 的天气现象出现增多.陡然降温幅度大于
的天气现象出现增多.陡然降温幅度大于![]() 容易引起幼儿伤风感冒疾病.为了解伤风感冒疾病是否与性别有关,在某妇幼保健院随机对人院的
容易引起幼儿伤风感冒疾病.为了解伤风感冒疾病是否与性别有关,在某妇幼保健院随机对人院的![]() 名幼儿进行调查,得到了如下的列联表,若在全部
名幼儿进行调查,得到了如下的列联表,若在全部![]() 名幼儿中随机抽取
名幼儿中随机抽取![]() 人,抽到患伤风感冒疾病的幼儿的概率为
人,抽到患伤风感冒疾病的幼儿的概率为![]() ,
,
(1)请将下面的列联表补充完整;
患伤风感冒疾病 | 不患伤风感冒疾病 | 合计 | |
男 | 25 | ||
女 | 20 | ||
合计 | 100 |
(2)能否在犯错误的概率不超过![]() 的情况下认为患伤风感冒疾病与性别有关?说明你的理由;
的情况下认为患伤风感冒疾病与性别有关?说明你的理由;
(3)已知在患伤风感冒疾病的![]() 名女性幼儿中,有
名女性幼儿中,有![]() 名又患黄痘病.现在从患伤风感冒疾病的
名又患黄痘病.现在从患伤风感冒疾病的![]() 名女性中,选出
名女性中,选出![]() 名进行其他方面的排查,记选出患黄痘病的女性人数为
名进行其他方面的排查,记选出患黄痘病的女性人数为![]() ,求
,求![]() 的分布列以及数学期望.下面的临界值表供参考:
的分布列以及数学期望.下面的临界值表供参考:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
参考公式: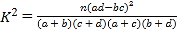 ,其中
,其中![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,一智能扫地机器人在A处发现位于它正西方向的B处和北偏东![]() 方向上的C处分别有需要清扫的垃圾,红外线感应测量发现机器人到B的距离比到C的距离少0.4m,于是选择沿
方向上的C处分别有需要清扫的垃圾,红外线感应测量发现机器人到B的距离比到C的距离少0.4m,于是选择沿![]() 路线清扫.已知智能扫地机器人的直线行走速度为0.2m/s,忽略机器人吸入垃圾及在B处旋转所用时间,10秒钟完成了清扫任务.
路线清扫.已知智能扫地机器人的直线行走速度为0.2m/s,忽略机器人吸入垃圾及在B处旋转所用时间,10秒钟完成了清扫任务.
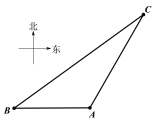
(1)B、C两处垃圾的距离是多少?(精确到0.1)
(2)智能扫地机器人此次清扫行走路线的夹角![]() 是多少?(用反三角函数表示)
是多少?(用反三角函数表示)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了配合今年上海迪斯尼游园工作,某单位设计了统计人数的数学模型![]() :以
:以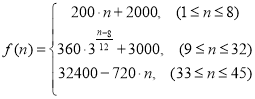 表示第
表示第![]() 个时刻进入园区的人数;以
个时刻进入园区的人数;以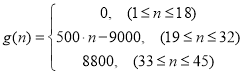 表示第
表示第![]() 个时刻离开园区的人数.设定以
个时刻离开园区的人数.设定以![]() 分钟为一个计算单位,上午
分钟为一个计算单位,上午![]() 点
点![]() 分作为第
分作为第![]() 个计算人数单位,即
个计算人数单位,即![]() ;
;![]() 点
点![]() 分作为第
分作为第![]() 个计算单位,即
个计算单位,即![]() ;依次类推,把一天内从上午
;依次类推,把一天内从上午![]() 点到晚上
点到晚上![]() 点
点![]() 分分成
分分成![]() 个计算单位(最后结果四舍五入,精确到整数).
个计算单位(最后结果四舍五入,精确到整数).
(1)试计算当天![]() 点至
点至![]() 点这一小时内,进入园区的游客人数
点这一小时内,进入园区的游客人数![]() 、离开园区的游客人数
、离开园区的游客人数![]() 各为多少?
各为多少?
(2)假设当日园区游客总人数达到或超过![]() 万时,园区将采取限流措施.该单位借助该数学模型知晓当天
万时,园区将采取限流措施.该单位借助该数学模型知晓当天![]() 点(即
点(即![]() )时,园区总人数会达到最高,请问当日是否要采取限流措施?说明理由.
)时,园区总人数会达到最高,请问当日是否要采取限流措施?说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com