练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】“众志成城，抗击疫情，一方有难，八方支援”，在此次抗击疫情过程中，各省市都派出援鄂医疗队. 假设汕头市选派名主任医生，名护士，组成三个医疗小组分配到湖北甲、乙、丙三地进行医疗支援，每个小组包括名主任医生和名护士，则不同的分配方案有（ ）

    A.种B.种C.种D.种

    【答案】C

    【解析】

    先求把6名医生平均分成3组的方法，再求将3组医生与3名护士进行全排列组成医疗小组的方法，最后求把3个医疗小组分到3个地方的方法，最后求积即可.

    解：分三步进行：

    （1）将6名医生分成3组，有种方法，

    （2）将分好的三组与三名女护士进行全排列，组成三个医疗小组有种方法，

    （3）将分好的三个医疗小组进行全排列，对应于甲、乙、丙三地有种方法，

    则不同的分配方案有种方法，

    故选：C.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

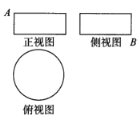
    【题目】某圆柱的高为2，底面周长为16，则其体积为_________，若该圆柱的三视图如图所示，圆柱表面上的点M在正视图上的对应点为A，圆柱表面上的点N在侧视图上的对应点为B，则在此圆柱侧面上，从M到N的路径中，最短路径的长度为___________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，已知直三棱柱ABC﹣A1B1C1，E，F分别是棱CC1，AB的中点．

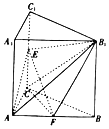
    （1）证明：CF∥平面AEB1．

    （2）若AC＝BC＝AA1＝4，∠ACB＝90°，求三棱锥B1﹣ECF的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在多面体中，两两垂直，四边形是边长为2的正方形，ACDGEF，且.

    （1）证明：平面.

    （2）求二面角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角梯形ABCD中（如图1），，，，，，点E在CD上，且，将沿AE折起，使得平面平面ABCE（如图2），G为AE中点．

    （Ⅰ）求四棱锥的体积；

    （Ⅱ）在线段BD上是否存在点P，使得平面ADE？若存在，求的值；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，若，则函数的零点个数为________；若函数有4个零点，则实数的取值范围是_______.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数

    （1）求函数的单调区间；

    （2）若，对恒成立，求实数的取值范围；

    （3）当时，设.若正实数，满足，，，证明：.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数在处的导数为，，

    （1）若不等式对任意恒成立，求实数的取值范围.

    （2）若在上有且只有一个零点，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】学校艺术节对四件参赛作品只评一件一等奖，在评奖揭晓前，甲，乙，丙，丁四位同学对这四件参赛作品预测如下：

    甲说：“是或作品获得一等奖”； 乙说：“ 作品获得一等奖”；

    丙说：“ 两件作品未获得一等奖”； 丁说：“是作品获得一等奖”．

    评奖揭晓后，发现这四位同学中只有两位说的话是对的，则获得一等奖的作品是_________．

    查看答案和解析>>

    同步练习册答案