
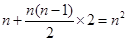 ,付出投资81万元,由此可知利润y=30n-(81+n2),由y>0能求出从第几年开始获取纯利润.
,付出投资81万元,由此可知利润y=30n-(81+n2),由y>0能求出从第几年开始获取纯利润.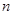 年获取利润为
年获取利润为 万元。………………1分
万元。………………1分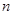 年共收租金30
年共收租金30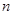 万元,付出装修费构成一个以1为首项,2为公差的等差数列,
万元,付出装修费构成一个以1为首项,2为公差的等差数列,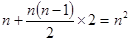 …………………2分
…………………2分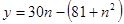 令
令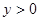 ……………4分
……………4分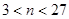 ……………5分
……………5分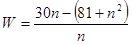 ………………8分
………………8分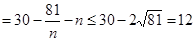 ………………9分
………………9分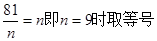 )所以9年后共获利润:154万元。……………10分
)所以9年后共获利润:154万元。……………10分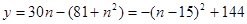


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:不详 题型:填空题
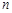 ,定义“
,定义“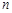
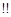 ”如下:当
”如下:当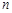 是偶数时,
是偶数时,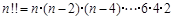 ,
, 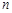 是奇数时,
是奇数时,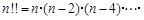
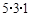 .现在有如下四个命题:
.现在有如下四个命题: 的个位数是0;
的个位数是0; 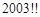 的个位数是5;
的个位数是5;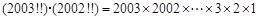 ;
; 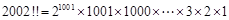 ;
;查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
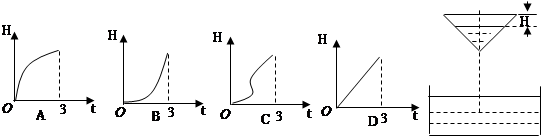
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com