
ЗжЮі ЃЈ1ЃЉгЩcos2Іе+sin2Іе=1ЃЌФмЧѓГіЧњЯпC2ЕФЦеЭЈЗНГЬЃЌЯШЧѓГіЧњЯпC1ЕФжБНЧзјБъЗНГЬЃЌгЩДЫФмЧѓГіЧњЯпC1ЕФМЋзјБъЯЕЗНГЬЃЎ
ЃЈ2ЃЉЩшЕуPЃЈ$cosІе\sqrt{3}sinІе$ЃЉЃЌгЩДЫРћгУЕуPЕНЧњЯпC1ОрРыЙЋЪНФмЧѓГіЕуPЕНЧњЯпC1ОрРыЕФзюаЁжЕЃЎ
НтД№ НтЃКЃЈ1ЃЉЁпЧњЯпC2ЕФВЮЪ§ЗНГЬЮЊЃК$\left\{\begin{array}{l}x=cosІе\\ y=\sqrt{3}sinІе\end{array}\right.$ЃЈІеЮЊВЮЪ§ЃЉЃЌ
ЁрЧњЯпC2ЕФЦеЭЈЗНГЬЮЊ${x}^{2}+\frac{{y}^{2}}{3}$=1ЃЌ
ЁпЧњЯпC1ЕФВЮЪ§ЗНГЬЮЊЃК$\left\{\begin{array}{l}x=1+tcos\frac{Іа}{4}\\ y=5+tsin\frac{Іа}{4}\end{array}\right.$ЃЈtЮЊВЮЪ§ЃЉЃЌ
ЁрЧњЯпC1ЕФжБНЧзјБъЗНГЬЮЊx-y+4=0ЃЌ
ЁрЧњЯпC1ЕФМЋзјБъЯЕЗНГЬЮЊІбcosІШ-ІбsinІШ+4=0ЃЎ
ЃЈ2ЃЉЁпЕуPЮЊЧњЯпC2ЩЯШЮвтвЛЕуЃЌЁрЩшЕуPЃЈ$cosІе\sqrt{3}sinІе$ЃЉЃЌ
ЁрЕуPЕНЧњЯпC1ОрРыЃКd=$\frac{|cosІе-\sqrt{3}sinІе+4|}{\sqrt{1+1}}$=$\frac{\sqrt{2}}{2}$|2sinЃЈІе+150ЁуЃЉ+4|ЃЌ
ЁрЕуPЕНЧњЯпC1ОрРыЕФзюаЁжЕЮЊdmin=$\frac{\sqrt{2}}{2}$|-2+4|=$\sqrt{2}$ЃЎ
ЕуЦР БОЬтПМВщВЮЪ§ЗНГЬЁЂЦеЭЈЗНГЬЁЂМЋзјБъЗНГЬЁЂжБНЧзјБъЗНГЬЕФЛЅЛЏЃЌПМВщЕуЕНЧњЯпЕФОрРыЕФзюаЁжЕЕФЧѓЗЈЃЌЪЧжаЕЕЬтЃЌНтЬтЪБвЊШЯецЩѓЬтЃЌзЂвтМЋзјБъКЭжБНЧзјБъЛЅЛЏЙЋЪНЕФКЯРэдЫгУЃЎ


 еуНУћаЃУћЪІН№ОэЯЕСаД№АИ
еуНУћаЃУћЪІН№ОэЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | ЕШбќШ§НЧаЮ | BЃЎ | жБНЧШ§НЧаЮ | CЃЎ | ЕШбќжБНЧШ§НЧаЮ | DЃЎ | ЕШБпШ§НЧаЮ |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
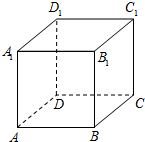 ШчЭМЃЌвбжЊе§ЗНЬхABCD-A1B1C1DЃЌШєдкЦф12ЬѕРтжаЫцЛњЕиШЁ3ЬѕЃЌдђетШ§ЬѕРтСНСНЪЧвьУцжБЯпЕФИХТЪЪЧ$\frac{2}{55}$ЃЈНсЙћгУзюМђЗжЪ§БэЪОЃЉ
ШчЭМЃЌвбжЊе§ЗНЬхABCD-A1B1C1DЃЌШєдкЦф12ЬѕРтжаЫцЛњЕиШЁ3ЬѕЃЌдђетШ§ЬѕРтСНСНЪЧвьУцжБЯпЕФИХТЪЪЧ$\frac{2}{55}$ЃЈНсЙћгУзюМђЗжЪ§БэЪОЃЉВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com