
【题目】如图,在三棱柱![]() 中,
中,![]() 平面
平面![]() ,点
,点![]() 是
是![]() 的中点,
的中点,![]() ,
,![]() ,
,![]() .
.
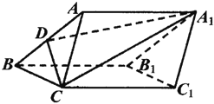
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求点![]() 到平面
到平面![]() 的距离.
的距离.
【答案】(1)证明见解析(2)![]()
【解析】
(1)通过证明![]() 证得
证得![]() 平面
平面![]() ,由此证得平面
,由此证得平面![]() 平面
平面![]() .
.
(2)解法一:利用等体积法计算出点![]() 到平面
到平面![]() 的距离;解法二:在平面
的距离;解法二:在平面![]() 内,过
内,过![]() 作
作![]() ,证得
,证得![]() 就是点
就是点![]() 到平面
到平面![]() 的距离,利用等面积法求得点
的距离,利用等面积法求得点![]() 到平面
到平面![]() 的距离.
的距离.
(1)证明:∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() ,
,
∵![]() ,
,![]() 是的
是的![]() 的中点,∴
的中点,∴![]() ,
,
又![]() ,∴
,∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() ;
;
(2)解法一∵![]() 平面
平面![]() ,∴
,∴![]() 是三棱锥
是三棱锥![]() 的高,
的高,
且![]() ,
,
由(1)及已知得![]() 是腰长为1的等腰直角三角形,
是腰长为1的等腰直角三角形,
![]() ,
,
∴![]() ,
,
又![]() ,所以
,所以![]() ,
,
由(1)得![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() ,
,
∴![]() ,设点
,设点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,
,
由![]() ,得
,得![]() ,
,
∴![]() 因此,点
因此,点![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.
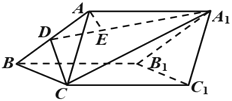
解法二:由(1)平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
在平面![]() 内,过
内,过![]() 作
作![]() ,则
,则![]() 平面
平面![]() ,故
,故![]() 就是点
就是点![]() 到平面
到平面![]() 的距离,
的距离,
∵![]() 平面
平面![]() ,∴在
,∴在![]() 中,
中,![]() .
.
利用等面积得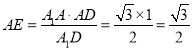 ,
,
因此,点![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:高中数学 来源: 题型:
【题目】下列说法正确的个数为( )
①命题“![]() 中,若
中,若![]() ,则
,则![]() ”的逆命题是真命题
”的逆命题是真命题
②若命题![]() ,则
,则![]()
③“命题![]() 为真命题”是“命题
为真命题”是“命题![]() 为假命题”的充要条件
为假命题”的充要条件
④设![]() 均为非零向量,则“
均为非零向量,则“![]() ”是“
”是“![]() 与
与![]() 的夹角为锐角”的必要不充分条件
的夹角为锐角”的必要不充分条件
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,过抛物线上一点
,过抛物线上一点![]() 作抛物线
作抛物线![]() 的切线
的切线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() ,当
,当![]() 时,
时,![]() .
.
(1)判断![]() 的形状,并求抛物线
的形状,并求抛物线![]() 的方程;
的方程;
(2)若![]() 两点在抛物线
两点在抛物线![]() 上,且满足
上,且满足![]() ,其中点
,其中点![]() ,若抛物线
,若抛物线![]() 上存在异于
上存在异于![]() 的点
的点![]() ,使得经过
,使得经过![]() 三点的圆和抛物线在点
三点的圆和抛物线在点![]() 处有相同的切线,求点
处有相同的切线,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从5名男生和4名女生中选出4人参加辩论比赛.
(1)如果男生中的甲与女生中的乙至少要有1人在内,那么有多少种不同选法?
(2)如果4个人中既有男生又有女生,那么有多少种不同选法?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某林场现有木材存量为![]() ,每年以25%的增长率逐年递增,但每年年底要砍伐的木材量为
,每年以25%的增长率逐年递增,但每年年底要砍伐的木材量为![]() ,经过
,经过![]() 年后林场木材存有量为
年后林场木材存有量为![]()
(1)求![]() 的解析式
的解析式
(2)为保护生态环境,防止水土流失,该地区每年的森林木材存量不应少于![]() ,如果
,如果![]() ,那么该地区会发生水土流失吗?若会,要经过几年?(取
,那么该地区会发生水土流失吗?若会,要经过几年?(取![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过点![]() 作已知直线
作已知直线![]() 的平行线,交双曲线
的平行线,交双曲线![]() 于点
于点![]() .
.
(1)证明:Q是线段MN的中点;
(2)分别过点M、N作双曲线的切线![]() ,证明:三条直线
,证明:三条直线![]() 相交于同一点;
相交于同一点;
(3)设![]() 为直线
为直线![]() 上一动点,过
上一动点,过![]() 作双曲线的切线
作双曲线的切线![]() ,切点分别为
,切点分别为![]() ,证明:点Q在直线AB上.
,证明:点Q在直线AB上.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com