
【题目】已知![]() 满足
满足 .
.
(1)求![]() 取到最值时的最优解;
取到最值时的最优解;
(2)求![]() 的取值范围;
的取值范围;
(3)若![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】有以下三个案例:
案例一:从同一批次同类型号的10袋牛奶中抽取3袋检测其三聚氰胺含量;
案例二:某公司有员工800人:其中高级职称的160人,中级职称的320人,初级职称200人,其余人员120人.从中抽取容量为40的样本,了解该公司职工收入情况;
案例三:从某校1000名学生中抽10人参加主题为“学雷锋,树新风”的志愿者活动.
(1)你认为这些案例应采用怎样的抽样方式较为合适?
(2)在你使用的分层抽样案例中写出每层抽样的人数;
(3)在你使用的系统抽样案例中按以下规定取得样本编号:如果在起始组中随机抽取的码为![]() (编号从0开始),那么第
(编号从0开始),那么第![]() 组(组号
组(组号![]() 从0开始,
从0开始,![]() )抽取的号码的百位数为组号,后两位数为
)抽取的号码的百位数为组号,后两位数为![]() 的后两位数.若
的后两位数.若![]() ,试求出
,试求出![]() 及
及![]() 时所抽取的样本编号.
时所抽取的样本编号.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l的方程为3x+4y﹣12=0,求直线l'的方程,使得:
(1)l'与l平行,且过点(﹣1,3);
(2)l'与l垂直,且l'与两轴围成的三角形面积为4.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,已知
中,已知![]() 底面
底面![]() ,异面直线
,异面直线![]() 和
和![]() 所成角等于
所成角等于![]() .
.
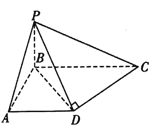
(1)求证: 平面![]() 平面
平面![]() ;
;
(2)求直线![]() 和平面
和平面![]() 所成角的正弦值;
所成角的正弦值;
(3) 在棱![]() 上是否存在一点
上是否存在一点![]() ,使得平面
,使得平面![]() 与平面
与平面![]() 所成锐二面角的正切值为
所成锐二面角的正切值为![]() ?若存在,指出点
?若存在,指出点![]() 在棱
在棱![]() 上的位置,若不存在,说明理由.
上的位置,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 是指大气中直径小于或等于
是指大气中直径小于或等于![]() 微米的颗粒物,也称为可入肺颗粒物,对人体健康和大气环境质量的影响很大.我国
微米的颗粒物,也称为可入肺颗粒物,对人体健康和大气环境质量的影响很大.我国![]() 标准采用世卫组织设定的最宽限值.即
标准采用世卫组织设定的最宽限值.即![]() 日均值在35微克/立方米以下空气质量为一级;在35微克/立方米
日均值在35微克/立方米以下空气质量为一级;在35微克/立方米![]() 75微克/立方米之间空气质量为二级;75微克/立方米以上空气质量为超标.
75微克/立方米之间空气质量为二级;75微克/立方米以上空气质量为超标.
某市环保局从360天的市区![]() 监测数据中统计了1月至10月的每月的平均值(单位:微克/立方米),如下表所示.
监测数据中统计了1月至10月的每月的平均值(单位:微克/立方米),如下表所示.
月份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 32 | 28 | 25 | 31 | 34 | 33 | 45 | 44 | 63 | 68 |
(1)从5月到10月的这6个数据中任取2个数值,求这个2个数值均为二级的概率;
(2)求月均值![]() 关于月份
关于月份![]() 的回归直线方程
的回归直线方程![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ),(A>0,ω>0,|φ|< ![]() )的部分图象如图所示.
)的部分图象如图所示. 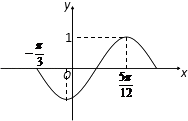
(1)求f(x)> ![]() 在x∈[0,π]上的解集;
在x∈[0,π]上的解集;
(2)设g(x)=2 ![]() cos2x+f(x),g(α)=
cos2x+f(x),g(α)= ![]() +
+ ![]() ,α∈(
,α∈( ![]() ,
, ![]() ),求sin2α的值.
),求sin2α的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}为等比数列,数列{bn}满足bn=na1+(n﹣1)a2+…+2an﹣1+an , n∈N* , 已知b1=m, ![]() ,其中m≠0.
,其中m≠0.
(1)求数列{an}的首项和公比;
(2)当m=1时,求bn;
(3)设Sn为数列{an}的前n项和,若对于任意的正整数n,都有Sn∈[1,3],求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ,g(x)=x2+2mx+
,g(x)=x2+2mx+ ![]()
(1)用定义法证明f(x)在R上是增函数;
(2)求出所有满足不等式f(2a﹣a2)+f(3)>0的实数a构成的集合;
(3)对任意的实数x1∈[﹣1,1],都存在一个实数x2∈[﹣1,1],使得f(x1)=g(x2),求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com