
【题目】如图,在四棱锥P﹣ABCD中,侧面PAD⊥底面ABCD,∠PAD=90°,CD∥AB,∠BAD=90°,且AB=3CD=3PA![]() AD=3.
AD=3.
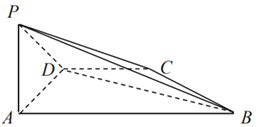
(1)求证:BD⊥PC;
(2)求点A到平面PCD的距离.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)连接AC,交BD于E,推导出AC⊥BD,PA⊥AD,从而PA⊥平面ABCD,PA⊥BD,进而BD⊥平面PAC,由此能证明BD⊥PC.
(2)由VA﹣PCD=VP﹣ACD,能求出点A到平面PCD的距离.
(1)证明:连接AC,交BD于E,
由已知,在Rt△DAB中,∠DBA=30°,在Rt△ADC中,∠DAC=30°,
∴∠CAB=60°,∴∠AEB=90°,∴AC⊥BD,
∵平面PAD⊥平面ABCD,平面![]() 平面
平面![]() ,PA⊥AD,
,PA⊥AD,![]() 平面
平面![]() ,∴PA⊥平面ABCD,
,∴PA⊥平面ABCD,
![]() 平面
平面![]() ,∴PA⊥BD,
,∴PA⊥BD,
∵AC∩PA=A,∴BD⊥平面PAC,
![]() 平面
平面![]() ,∴BD⊥PC;
,∴BD⊥PC;
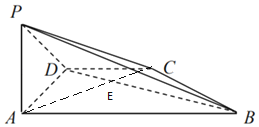
(2)解:设点![]() 到面
到面![]() 的距离为
的距离为![]() ,点
,点![]() 到面
到面![]() 的距离为
的距离为![]() ,
,
∵VA﹣PCD=VP﹣ACD,∴![]() ,
,
∵PA⊥平面ACD,∴hP=PA=1,
∴![]() ,
,
解得点A到平面PCD的距离hA![]() .
.


科目:高中数学 来源: 题型:
【题目】《算法统宗》全称《新编直指算法统宗》,是屮国古代数学名著,程大位著.书中有如下问题:“今有五人均银四十两,甲得十两四钱,戊得五两六钱.问:次第均之,乙丙丁各该若干?”意思是:有5人分40两银子,甲分10两4钱,戊分5两6钱,且相邻两项差相等,则乙丙丁各分几两几钱?(注:1两等于10钱)( )
A.乙分8两,丙分8两,丁分8两B.乙分8两2钱,丙分8两,丁分7两8钱
C.乙分9两2钱,丙分8两,丁分6两8钱D.乙分9两,丙分8两,丁分7两
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两个无穷数列![]() 分别满足
分别满足![]() ,
,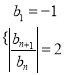 ,
,
其中![]() ,设数列
,设数列![]() 的前
的前![]() 项和分别为
项和分别为![]() ,
,
(1)若数列![]() 都为递增数列,求数列
都为递增数列,求数列![]() 的通项公式;
的通项公式;
(2)若数列![]() 满足:存在唯一的正整数
满足:存在唯一的正整数![]() (
(![]() ),使得
),使得![]() ,称数列
,称数列![]() 为“
为“![]() 坠点数列”
坠点数列”
①若数列![]() 为“5坠点数列”,求
为“5坠点数列”,求![]() ;
;
②若数列![]() 为“
为“![]() 坠点数列”,数列
坠点数列”,数列![]() 为“
为“![]() 坠点数列”,是否存在正整数
坠点数列”,是否存在正整数![]() ,使得
,使得![]() ,若存在,求
,若存在,求![]() 的最大值;若不存在,说明理由.
的最大值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的离心率
的离心率![]() ,若椭圆的左、右焦点分别为
,若椭圆的左、右焦点分别为![]() ,
,![]() ,椭圆上一动点
,椭圆上一动点![]() 和
和![]() ,
,![]() 组成
组成![]() 的面积最大为
的面积最大为![]() .
.
(1)求椭圆的方程;
(2)若存在直线![]() :
:![]() 和椭圆相交于不同的两点
和椭圆相交于不同的两点![]() ,
,![]() ,且原点
,且原点![]() 与
与![]() ,
,![]() 连线的斜率之和满足:
连线的斜率之和满足:![]() .求直线
.求直线![]() 的斜率
的斜率![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱锥![]() ,侧棱
,侧棱![]() ,底面三角形
,底面三角形![]() 为正三角形,边长为
为正三角形,边长为![]() ,顶点
,顶点![]() 在平面
在平面![]() 上的射影为
上的射影为![]() ,有
,有![]() ,且
,且![]() .
.
(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)线段![]() 上是否存在点
上是否存在点![]() 使得
使得![]() ⊥平面
⊥平面![]() ,如果存在,求
,如果存在,求![]() 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥![]() 的底面为正方形,且该四棱锥的每条棱长均为
的底面为正方形,且该四棱锥的每条棱长均为![]() ,设BC,CD的中点分别为E,F,点G在线段PA上,如图.
,设BC,CD的中点分别为E,F,点G在线段PA上,如图.
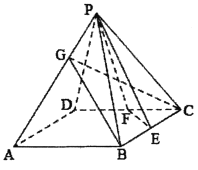
(1)证明:![]() ;
;
(2)当![]() 平面PEF时,求直线GC和平面PEF所成角的正弦值.
平面PEF时,求直线GC和平面PEF所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的图象过点
的图象过点![]() 和点
和点![]() .
.
(1)求函数![]() 的最大值与最小值;
的最大值与最小值;
(2)将函数![]() 的图象向左平移
的图象向左平移![]() 个单位后,得到函数
个单位后,得到函数![]() 的图象;已知点
的图象;已知点![]() ,若函数
,若函数![]() 的图象上存在点
的图象上存在点![]() ,使得
,使得![]() ,求函数
,求函数![]() 图象的对称中心.
图象的对称中心.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,
,![]() 是坐标轴上两点,动点
是坐标轴上两点,动点![]() 满足直线
满足直线![]() 与
与![]() 的斜率之积为
的斜率之积为![]() (其中
(其中![]() 为常数,且
为常数,且![]() ).记
).记![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求![]() 的方程,并说明
的方程,并说明![]() 是什么曲线;
是什么曲线;
(2)过点![]() 斜率为
斜率为![]() 的直线与曲线
的直线与曲线![]() 交于点
交于点![]() ,点
,点![]() 在曲线
在曲线![]() 上,且
上,且![]() ,若
,若![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com