
分析 椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率为$\frac{{\sqrt{3}}}{2}$,故设椭圆方程为$\frac{{x}^{2}}{4{λ}^{2}}+\frac{{y}^{2}}{{λ}^{2}}=1$,λ>0,
联立$\left\{\begin{array}{l}{\frac{{x}^{2}}{4{λ}^{2}}+\frac{{y}^{2}}{{λ}^{2}}=1}\\{x-y+1=0}\end{array}\right.$,得5x2+8x+4-4λ2=0,设A(x1,y1),B(x2,y2),
${x}_{1}+{x}_{2}=-\frac{8}{5},{x}_{1}{x}_{2}=\frac{4-4{λ}^{2}}{5}$,…①,C(0,1),$3\overrightarrow{AB}=2\overrightarrow{BC}$,可得5x2=3x1.…②,把②代入①得λ2
解答 解:∵椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率为$\frac{{\sqrt{3}}}{2}$,
∴$e=\frac{c}{a}=\frac{\sqrt{3}}{2}$,设a=2λ,(λ>0),则c=$\sqrt{3}λ$,b=λ,
∴椭圆方程为$\frac{{x}^{2}}{4{λ}^{2}}+\frac{{y}^{2}}{{λ}^{2}}=1$,λ>0,
联立$\left\{\begin{array}{l}{\frac{{x}^{2}}{4{λ}^{2}}+\frac{{y}^{2}}{{λ}^{2}}=1}\\{x-y+1=0}\end{array}\right.$,得5x2+8x+4-4λ2=0,
△>0,设A(x1,y1),B(x2,y2),
${x}_{1}+{x}_{2}=-\frac{8}{5},{x}_{1}{x}_{2}=\frac{4-4{λ}^{2}}{5}$,…①,C(0,1),
∵$3\overrightarrow{AB}=2\overrightarrow{BC}$,∴5x2=3x1.…②,把②代入①得λ2=$\frac{1}{4}$,
可得x2+4y2=1.
故答案为:x2+4y2=1.
点评 本题考查了椭圆与直线的位置关系,关键是要把向量式转化为坐标关系,利用韦达定理,属于中档题.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:选择题
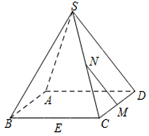 如图,在正四棱锥S-ABCD中,E,M,N分别是BC,CD,SC的中点,动点P在线段MN上运动时,下列四个结论:
如图,在正四棱锥S-ABCD中,E,M,N分别是BC,CD,SC的中点,动点P在线段MN上运动时,下列四个结论:| A. | ①③ | B. | ③④ | C. | ①② | D. | ②③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
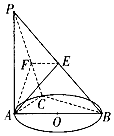 如图所示,PA垂直于圆O所在平面,AB是圆O的直径,C是圆O上一点,点A在PB,PC上的射影分别为E,F,则以下结论错误的是( )
如图所示,PA垂直于圆O所在平面,AB是圆O的直径,C是圆O上一点,点A在PB,PC上的射影分别为E,F,则以下结论错误的是( )| A. | PB⊥AF | B. | PB⊥EF | C. | AF⊥BC | D. | AE⊥BC |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4033 | B. | -4033 | C. | 8066 | D. | -8066 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,+∞) | B. | (1,+∞) | C. | (-∞,-1]∪[1,+∞) | D. | (-∞,-1)∪(1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com