
| A、[1,+∞) | ||
B、[1,
| ||
| C、[1,2) | ||
D、[
|
| 1 |
| 2 |
|
| 1 |
| x |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
|
| 3 |
| 2 |


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:
| 3 |
| π |
| 2 |
| π |
| 2 |
| A、y=f(x)的最小正周期为2π,且在(0,π)上为增函数 | ||
| B、y=f(x)的最小正周期为π,且在 (0,π)上为减函数 | ||
C、y=f(x)的最小正周期为π,且在(0,
| ||
D、y=f(x)的最小正周期为π,且在(0,
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、f′(x)就是曲线f(x)在点(x0,f(x0))的切线的斜率 |
| B、f′(x0)与(f(x0))′意义是一样的 |
| C、设s=s(t)是位移函数,则s′(t0)表示物体在t=t0时刻的瞬时速度 |
| D、设v=v(t)是速度函数,则v′(t0)表示物体在t=t0时刻的加速度 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、简单随机抽样是一种逐个抽取不放回的抽样 |
| B、系统抽样和分层抽样中每个个体被抽到的概率都相等 |
| C、有2008个零件,先用随机数表法剔除8个,再用系统抽样方法抽取抽取20个作为样本,每个零件入选样本的概率都为1/2000 |
| D、当总体是由差异明显的几个部分组成时适宜采取分层抽样 |
查看答案和解析>>
科目:高中数学 来源: 题型:
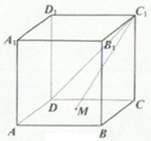 如图所示正方体ABCD-A1B1C1D1,设M是底面正方形ABCD内的一个动点,且满足直线C1D与直线C1M所成的角等于30°,则以下说法正确的是( )
如图所示正方体ABCD-A1B1C1D1,设M是底面正方形ABCD内的一个动点,且满足直线C1D与直线C1M所成的角等于30°,则以下说法正确的是( )| A、点M的轨迹是圆的一部分 |
| B、点M的轨迹是椭圆的一部分 |
| C、点M的轨迹是双曲线的一部分 |
| D、点M的轨迹是抛物线的一部分 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、a≥0 | B、a<0 |
| C、b≤0 | D、b>1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、16π | B、32π |
| C、64π | D、128π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com