
【题目】一种掷硬币走跳棋的游戏:在棋盘上标有第1站、第2站、第3站、…、第100站,共100站,设棋子跳到第![]() 站的概率为
站的概率为![]() ,一枚棋子开始在第1站,棋手每掷一次硬币,棋子向前跳动一次.若硬币的正面向上,棋子向前跳一站;若硬币的反面向上,棋子向前跳两站,直到棋子跳到第99站(失败)或者第100站(获胜)时,游戏结束.
,一枚棋子开始在第1站,棋手每掷一次硬币,棋子向前跳动一次.若硬币的正面向上,棋子向前跳一站;若硬币的反面向上,棋子向前跳两站,直到棋子跳到第99站(失败)或者第100站(获胜)时,游戏结束.
(1)求![]()
![]()
![]() ;
;
(2)求证:数列![]()
![]() 为等比数列;
为等比数列;
(3)求玩该游戏获胜的概率.
【答案】(1)![]() ,
,![]() ,
,![]() (2)证明见解析 (3)
(2)证明见解析 (3)![]()
【解析】
(1)根据题意,分析可得棋子在1站是一个必然事件,即可得P1的值,进而分析棋子跳到2站以及棋子跳到3站的情况,据此求出P2、P3的值(2)根据题意,分析可得![]() ,变形可得
,变形可得![]() ,即可得结论(3)由(2)知
,即可得结论(3)由(2)知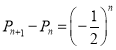 ,利用累加法求出
,利用累加法求出![]() ,由对立事件的概率性质求出
,由对立事件的概率性质求出![]() .
.
(1)棋子开始在第1站是必然事件,![]() ;
;
棋子跳到第2站,只有一种情况,第一次掷硬币正面向上,
其概率为![]()
![]() ;
;
棋子跳到第3站,有两种情况,①第一次掷硬币反面向上,其概率为![]() ;②前两次掷硬币都是正面向上,其概率为
;②前两次掷硬币都是正面向上,其概率为![]()
![]() ;
;
(2)棋子棋子跳到第![]()
![]() 站,有两种情况:①棋子先跳到第n站,又掷硬币反面向上,其概率为
站,有两种情况:①棋子先跳到第n站,又掷硬币反面向上,其概率为![]() ;②棋子先跳到第
;②棋子先跳到第![]() 站,又掷硬币正面向上,其概率为
站,又掷硬币正面向上,其概率为![]() .故
.故![]() .
.
![]()
又![]() ,
,
数列![]() …
…![]() 是以
是以![]() 为首项,
为首项,![]() 为公比的等比数列.
为公比的等比数列.
(3)由(2)得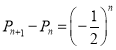 .
.
![]() …
…![]()
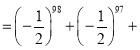 …
…![]()
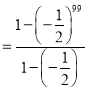
![]()
所以获胜的概率为![]()


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax+blnx(a,b∈R)在点(1,f(1))处的切线方程为y![]() x﹣1.
x﹣1.
(1)求ab的值;
(2)当x>1时,f(x)![]() 0恒成立,求实数k的取值范围;
0恒成立,求实数k的取值范围;
(3)设g(x)=ex![]() x,求证:对于x∈(0,+∞),g(x)﹣f(x)>2恒成立.
x,求证:对于x∈(0,+∞),g(x)﹣f(x)>2恒成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() ,
,![]() 是两条不同的直线,
是两条不同的直线,![]() ,
,![]() ,
,![]() 是三个不同的平面,给出下列四个命题:
是三个不同的平面,给出下列四个命题:
①若![]() ,
,![]() ,则
,则![]()
②若![]() ,
,![]() ,
,![]() ,则
,则![]()
③若![]() ,
,![]() ,则
,则![]()
④若![]() ,
,![]() ,则
,则![]()
其中正确命题的序号是( )
A.①和②B.②和③C.③和④D.①和④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】追求人类与生存环境的和谐发展是中国特色社会主义生态文明的价值取向.为了改善空气质量,某城市环保局随机抽取了一年内100天的空气质量指数(![]() )的检测数据,结果统计如下:
)的检测数据,结果统计如下:
|
|
|
|
|
|
|
空气质量 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
天数 | 6 | 14 | 18 | 27 | 25 | 10 |
(1)从空气质量指数属于![]() ,
,![]() 的天数中任取3天,求这3天中空气质量至少有2天为优的概率;
的天数中任取3天,求这3天中空气质量至少有2天为优的概率;
(2)已知某企业每天的经济损失![]() (单位:元)与空气质量指数
(单位:元)与空气质量指数![]() 的关系式为
的关系式为 ,试估计该企业一个月(按30天计算)的经济损失的数学期望.
,试估计该企业一个月(按30天计算)的经济损失的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,楔形几何体![]() 由一个三棱柱截去部分后所得,底面
由一个三棱柱截去部分后所得,底面![]() 侧面
侧面![]() ,
,![]() ,楔面
,楔面![]() 是边长为2的正三角形,点
是边长为2的正三角形,点![]() 在侧面
在侧面![]() 的射影是矩形
的射影是矩形![]() 的中心
的中心![]() ,点
,点![]() 在
在![]() 上,且
上,且![]()
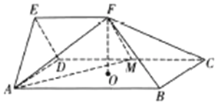
(1)证明:![]() 平面
平面![]() ;
;
(2)求楔面![]() 与侧面
与侧面![]() 所成二面角的余弦值.
所成二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某生产旅游纪念品的工厂,拟在2017年度进行系列促销活动.经市场调查和测算,该纪念品的年销售量x(单位:万件)与年促销费用t(单位:万元)之间满足3-x与t+1成反比例.若不搞促销活动,纪念品的年销售量只有1万件.已知工厂2017年生产纪念品的固定投资为3万元,每生产1万件纪念品另外需要投资32万元.当工厂把每件纪念品的售价定为“年平均每件生产成本的1.5倍”与“年平均每件所占促销费的一半”之和时,则当年的产量和销量相等.(利润=收入-生产成本-促销费用)
(1)请把该工厂2017年的年利润y(单位:万元)表示成促销费t(单位:万元)的函数;
(2)试问:当2017年的促销费投入多少万元时,该工厂的年利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,无穷数列
,无穷数列![]() 的首项
的首项![]() .
.
(1)如果![]() ,写出数列
,写出数列![]() 的通项公式;
的通项公式;
(2)如果![]() (
(![]() 且
且![]() ),要使得数列
),要使得数列![]() 是等差数列,求首项
是等差数列,求首项![]() 的取值范围;
的取值范围;
(3)如果![]() (
(![]() 且
且![]() ),求出数列
),求出数列![]() 的前
的前![]() 项和
项和![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地计划在一处海滩建造一个养殖场.
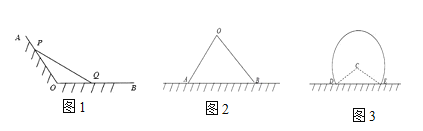
(1)如图1,射线OA,OB为海岸线,![]() ,现用长度为1千米的围网PQ依托海岸线围成一个
,现用长度为1千米的围网PQ依托海岸线围成一个![]() 的养殖场,问如何选取点P,Q,才能使养殖场
的养殖场,问如何选取点P,Q,才能使养殖场![]() 的面积最大,并求其最大面积.
的面积最大,并求其最大面积.
(2)如图2,直线l为海岸线,现用长度为1千米的围网依托海岸线围成一个养殖场.方案一:围成三角形OAB(点A,B在直线l上),使三角形OAB面积最大,设其为![]() ;方案二:围成弓形CDE(点D,E在直线l上,C是优弧所在圆的圆心且
;方案二:围成弓形CDE(点D,E在直线l上,C是优弧所在圆的圆心且![]() ),其面积为
),其面积为![]() ;试求出
;试求出![]() 的最大值和
的最大值和![]() (均精确到0.01平方千米),并指出哪一种设计方案更好.
(均精确到0.01平方千米),并指出哪一种设计方案更好.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com