【题目】如图，在四棱锥P-ABCD中，AB//CD，且
（1）证明：平面PAB⊥平面PAD；
（2）若PA=PD=AB=DC, 
,且四棱锥P-ABCD的体积为
，求该四棱锥的侧面积.
【答案】（1）见解析；（2）
.
【解析】试题分析：（1）由
， 
，得
平面
即可证得结果；（2）设
，则四棱锥
的体积
，解得
，可得所求侧面积．
试题解析：（1）由已知
，得
, 
.
由于
，故
，从而
平面
.
又
平面
，所以平面
平面
.
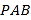
（2）在平面
内作
，垂足为
.
由（1）知， 
平面
，故
，可得
平面
.
设
，则由已知可得
， 
.
故四棱锥
的体积
.
由题设得
，故
.
从而
， 
， 
.
可得四棱锥
的侧面积为
.
点睛:证明面面垂直，先由线线垂直证明线面垂直，再由线面垂直证明面面垂直；计算点面距离时，如直接求不方便，应首先想到转化，如平行转化、对称转化、比例转化等，找到方便求值时再计算，可以减少运算量，提高准确度，求点面距离有时能直接作出就直接求出，不方便直接求出的看成三棱锥的高，利用等体积法求出．
科目：高中数学 来源： 题型：
【题目】定义在R上的奇函数f（x）满足f（x﹣2）=f（x+2），且当x∈[﹣2，0]时，f（x）=3x﹣1，则f（9）=（ ）
A.﹣2
B.2
C.
D.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在发生某公共卫生事件期间,有专业机构认为该事件在一段时间没有发生大规模群体感染的标准为“连续10天,每天新增疑似病例不超过7人”.根据过去10天甲、乙、丙、丁四地新增疑似病例的数据,一定符合该标准的是____.(填序号)
①甲地:总体均值为3,中位数为4
②乙地:总体均值为1,总体方差大于0
③丙地:中位数为2,众数为3
④丁地:总体均值为2,总体方差为3
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）是定义在R上的周期为2的奇函数，当0＜x＜1时，f（x）=2x（1﹣x），则f（﹣ 
）+f（1）=（ ）
A.﹣ 
B.﹣ 
C.
D.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】袋子中放有大小和形状相同的小球若干个,其中标号为0的小球1个,标号为1的小球1个,标号为2的小球n个.已知从袋子中随机抽取1个小球,取到标号是2的小球的概率是
.
(1)求n的值;
(2)从袋子中不放回地随机抽取2个小球,记第一次取出的小球标号为a,第二次取出的小球标号为b.
①记事件A表示“a+b=2”,求事件A的概率;
②在区间[0,2]内任取2个实数x,y,求事件“x2+y2>(a-b)2恒成立”的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.
根据该折线图,下列结论错误的是( )
A. 月接待游客量逐月增加
B. 年接待游客量逐年增加
C. 各年的月接待游客量高峰期大致在7,8月
D. 各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=lnx，g（x）= 
ax+b．
（1）若f（x）与g（x）在x=1处相切，试求g（x）的表达式；
（2）若φ（x）= 
﹣f（x）在[1，+∞）上是减函数，求实数m的取值范围．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
