
【题目】已知x=1是函数f(x)=![]() ax3-
ax3-![]() x2+(a+1)x+5的一个极值点.
x2+(a+1)x+5的一个极值点.
(1)求函数f(x)的解析式;
(2)若曲线y=f(x)与直线y=2x+m有三个交点,求实数m的取值范围.
【答案】(1)f(x)的解析式为f(x)=![]() x3-
x3-![]() x2+2x+5; (2)m的取值范围为
x2+2x+5; (2)m的取值范围为![]()
【解析】试题分析:(I)利用三次函数在极值点处的导数为零,即可解得a的值,进而确定函数的解析式;(II)将两曲线有三个交点问题,转化为函数g(x)=f(x)﹣(2x+m)有三个零点问题,利用导数研究函数g(x)的单调性和极值,找到问题的充要条件,列不等式即可解得m的范围
试题解析:
解:(1)依题意f′(x)=ax2-3x+a+1,
由f′(1)=0得a=1,
∴函数f(x)的解析式为f(x)=![]() x3-
x3-![]() x2+2x+5.
x2+2x+5.
(2)曲线y=f(x)与直线y=2x+m有三个交点,
即![]() x3-
x3-![]() x2+2x+5-2x-m=0有三个实数根,
x2+2x+5-2x-m=0有三个实数根,
令g(x)=![]() x3-
x3-![]() x2+2x+5-2x-m=
x2+2x+5-2x-m=![]() x3-
x3-![]() x2+5-m,则g(x)有三个零点.
x2+5-m,则g(x)有三个零点.
由g′(x)=x2-3x=0得x=0或x=3.
令g′(x)>0得x<0或x>3;令g′(x)<0得0<x<3.
∴函数g(x)在(-∞,0)上为增函数,在(0,3)上为减函数,在(3,+∞)上为增函数.
∴函数在x=0处取得极大值,在x=3处取得极小值.
要使g(x)有三个零点,只需 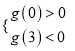 解得
解得![]() <m<5.
<m<5.
∴实数m的取值范围为![]() .
.


科目:高中数学 来源: 题型:
【题目】在△ABC中,角A、B、C所对的边分别是a、b、c满足:cosAcosC+sinAsinC+cosB= ![]() ,且a,b,c成等比数列,
,且a,b,c成等比数列,
(1)求角B的大小;
(2)若 ![]() +
+ ![]() =
= ![]() ,a=2,求三角形ABC的面积.
,a=2,求三角形ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= 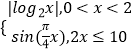 ,若存在实数x1 , x2 , x3 , x4 满足f(x1)=f(x2)=f(x3)=f(x4),且x1<x2<x3<x4 , 则
,若存在实数x1 , x2 , x3 , x4 满足f(x1)=f(x2)=f(x3)=f(x4),且x1<x2<x3<x4 , 则 ![]() 的取值范围是( )
的取值范围是( )
A.(20,32)
B.(9,21)
C.(8,24)
D.(15,25)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=-![]() x3+x2+(m2-1)x(x∈R),其中m>0.
x3+x2+(m2-1)x(x∈R),其中m>0.
(1)当m=1时,求曲线y=f(x)在点(1,f(1))处的切线斜率;
(2)求函数的单调区间与极值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列判断正确的是( )
A.a=7,b=14,A=30°,有两解
B.a=30,b=25,A=150°,有一解
C.a=6,b=9,A=45°,有两解
D.a=9,b=10,A=60°,无解
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1= ![]() ,an=
,an= ![]() (n≥2,n∈N).
(n≥2,n∈N).
(1)试判断数列 ![]() 是否为等比数列,并说明理由;
是否为等比数列,并说明理由;
(2)设bn= ![]() ,求数列{bn}的前n项和Sn;
,求数列{bn}的前n项和Sn;
(3)设cn=ansin ![]() ,数列{cn}的前n项和为Tn . 求证:对任意的n∈N* , Tn<
,数列{cn}的前n项和为Tn . 求证:对任意的n∈N* , Tn< ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com