
【题目】已知点A( ![]() +1,0),B(0,2).若直线l:y=k(x﹣1)+1与线段AB相交,则直线l倾斜角α的取值范围是( )
+1,0),B(0,2).若直线l:y=k(x﹣1)+1与线段AB相交,则直线l倾斜角α的取值范围是( )
A.[ ![]() ,
, ![]() ]
]
B.[0, ![]() ]
]
C.[0, ![]() ]∪[
]∪[ ![]() ,π)
,π)
D.[ ![]() ,π)
,π)
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A、B、C所对的边长分别为a,b,c且满足csinA= ![]() acosC,则sinA+sinB的最大值是( )
acosC,则sinA+sinB的最大值是( )
A.1
B.![]()
C.3
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了解一个英语教改实验班的情况,举行了一次测试,将该班30位学生的英语成绩进行统计,得图示频率分布直方图,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100]. 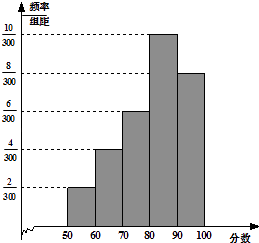
(1)求出该班学生英语成绩的众数,平均数及中位数;
(2)从成绩低于80分的学生中随机抽取2人,规定抽到的学生成绩在[50,60)的记1绩点分,在[60,80)的记2绩点分,设抽取2人的总绩点分为ξ,求ξ的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnax﹣ ![]() (a≠0).
(a≠0).
(1)求此函数的单调区间及最值;
(2)求证:对于任意正整数n,均有1+ ![]() +
+ ![]() …+
…+ ![]() ≥ln
≥ln ![]() (e为自然对数的底数).
(e为自然对数的底数).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣a|.
(1)若f(x)≤m的解集为{x|﹣1≤x≤5},求实数a,m的值.
(2)当a=2且0≤t<2时,解关于x的不等式f(x)+t≥f(x+2).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分为16分)设A,B分别为椭圆![]()
![]() 的左、右顶点,椭圆的长轴长为
的左、右顶点,椭圆的长轴长为![]() ,且点
,且点![]() 在该椭圆上.
在该椭圆上.
(1)求椭圆的方程;
(2)设![]() 为直线
为直线![]() 上不同于点
上不同于点![]() 的任意一点,若直线
的任意一点,若直线![]() 与椭圆相交于异于
与椭圆相交于异于![]() 的点
的点![]() ,证明:△
,证明:△![]() 为钝角三角形.
为钝角三角形.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分10分)设![]() 个正数
个正数![]() 满足
满足![]() (
(![]() 且
且![]() ).
).
(1)当![]() 时,证明:
时,证明:![]() ;
;
(2)当![]() 时,不等式
时,不等式![]() 也成立,请你将其推广到
也成立,请你将其推广到![]() (
(![]() 且
且![]() )个正数
)个正数![]() 的情形,归纳出一般性的结论并用数学归纳法证明.
的情形,归纳出一般性的结论并用数学归纳法证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() ,点B是其下顶点,过点B的直线交椭圆C于另一点A(A点在
,点B是其下顶点,过点B的直线交椭圆C于另一点A(A点在![]() 轴下方),且线段AB的中点E在直线
轴下方),且线段AB的中点E在直线![]() 上.
上.
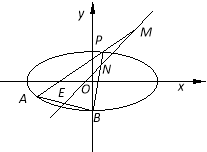
(1)求直线AB的方程;
(2)若点P为椭圆C上异于A、B的动点,且直线AP,BP分别交直线![]() 于点M、N,证明:OM·ON为定值.
于点M、N,证明:OM·ON为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com