
【题目】某礼品店要制作一批长方体包装盒,材料是边长为![]() 的正方形纸板.如图所示,先在其中相邻两个角处各切去一个边长是
的正方形纸板.如图所示,先在其中相邻两个角处各切去一个边长是![]() 的正方形,然后在余下两个角处各切去一个长、宽分别为
的正方形,然后在余下两个角处各切去一个长、宽分别为![]() 、
、![]() 的矩形,再将剩余部分沿图中的虚线折起,做成一个有盖的长方体包装盒.
的矩形,再将剩余部分沿图中的虚线折起,做成一个有盖的长方体包装盒.

(1)求包装盒的容积![]() 关于
关于![]() 的函数表达式,并求函数的定义域;
的函数表达式,并求函数的定义域;
(2)当![]() 为多少时,包装盒的容积最大?最大容积是多少?
为多少时,包装盒的容积最大?最大容积是多少?
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=2px(p>0)的焦点为F,A为C上异于原点的任意一点,过点A的直线l交C于另一点B,交x轴的正半轴于点D,且有丨FA丨=丨FD丨.当点A的横坐标为3时,△ADF为正三角形.
(1)求C的方程;
(2)若直线l1∥l,且l1和C有且只有一个公共点E,
(ⅰ)证明直线AE过定点,并求出定点坐标;
(ⅱ)△ABE的面积是否存在最小值?若存在,请求出最小值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,
,![]() 是函数
是函数![]() (
(![]() ,
,![]() )图象上的任意两点,且角
)图象上的任意两点,且角![]() 的终边经过点
的终边经过点![]() ,若
,若![]() 时,
时,![]() 的最小值为
的最小值为![]() .
.
(1)求函数![]() 的解析式;
的解析式;
(2)当![]() 时,不等式
时,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是一个半圆形湖面景点的平面示意图.已知![]() 为直径,且
为直径,且![]() km,
km,![]() 为圆心,
为圆心,![]() 为圆周上靠近
为圆周上靠近![]() 的一点,
的一点,![]() 为圆周上靠近
为圆周上靠近![]() 的一点,且
的一点,且![]() ∥
∥![]() .现在准备从
.现在准备从![]() 经过
经过![]() 到
到![]() 建造一条观光路线,其中
建造一条观光路线,其中![]() 到
到![]() 是圆弧
是圆弧![]() ,
,![]() 到
到![]() 是线段
是线段![]() .设
.设![]() ,观光路线总长为
,观光路线总长为![]() .
.

(1)求![]() 关于
关于![]() 的函数解析式,并指出该函数的定义域;
的函数解析式,并指出该函数的定义域;
(2)求观光路线总长的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,F1 , F2分别为椭圆 ![]() +
+ ![]() =1(a>b>0)的左、右焦点,顶点B的坐标为(0,b),连接BF2并延长交椭圆于点A,过点A作x轴的垂线交椭圆于另一点C,连接F1C.
=1(a>b>0)的左、右焦点,顶点B的坐标为(0,b),连接BF2并延长交椭圆于点A,过点A作x轴的垂线交椭圆于另一点C,连接F1C. 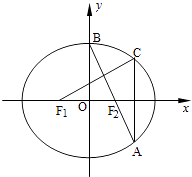
(1)若点C的坐标为( ![]() ,
, ![]() ),且BF2=
),且BF2= ![]() ,求椭圆的方程;
,求椭圆的方程;
(2)若F1C⊥AB,求椭圆离心率e的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn , 若对任意的正整数n,总存在正整数m,使得Sn=am , 则称{an}是“H数列”.
(1)若数列{an}的前n项和为Sn=2n(n∈N*),证明:{an}是“H数列”;
(2)设{an}是等差数列,其首项a1=1,公差d<0,若{an}是“H数列”,求d的值;
(3)证明:对任意的等差数列{an},总存在两个“H数列”{bn}和{cn},使得an=bn+cn(n∈N*)成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,倾斜角为 ![]() 的直线l与曲线C:
的直线l与曲线C: ![]() ,(α为参数)交于A,B两点,且|AB|=2,以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,则直线l的极坐标方程是 .
,(α为参数)交于A,B两点,且|AB|=2,以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,则直线l的极坐标方程是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校举办的集体活动中,设计了如下有奖闯关游戏:参赛选手按第一关、第二关、第三关的顺序依次闯关,若闯关成功,分别获得1分、2分、3分的奖励,游戏还规定,当选手闯过一关后,可以选择得到相应的分数,结束游戏;也可以选择继续闯下一关,若有任何一关没有闯关成功,则全部分数都归零,游戏结束。设选手甲第一关、第二关、第三关的概率分别为![]() ,
,![]() ,
,![]() ,选手选择继续闯关的概率均为
,选手选择继续闯关的概率均为![]() ,且各关之间闯关成功互不影响
,且各关之间闯关成功互不影响
(I)求选手甲第一关闯关成功且所得分数为零的概率
(II)设该学生所得总分数为X,求X的分布列与数学期望
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com