


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2013-2014学年浙江省浙北名校联盟高三上学期期中联考文科数学试卷(解析版) 题型:选择题
已知两个不重合的平面 和两条不同直线
和两条不同直线 ,则下列说法正确的是( )
,则下列说法正确的是( )
A. 若 则
则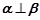
B. 若 则
则
C. 若 则
则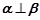
D. 若 则
则
查看答案和解析>>
科目:高中数学 来源:2010-2011学年广东省高三综合测试数学理卷 题型:选择题
已知两个不重合的平面α和β,下面给出四个条件:
①α内有无穷多条直线均与平面β平行;
②平面α,β均与平面γ平行;
③平面α,β与平面γ都相交,且其交线平行;
④平面α,β与直线l所成的角相等.
其中能推出α∥β的是( )
A.① B,② C.①和③ D.③和④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com