
【题目】某市自来水公司每两个月(记为一个收费周期)对用户收一次水费,收费标准如下:当每户用水量不超过![]() 吨时,按每吨
吨时,按每吨![]() 元收取;当该用户用水量超过
元收取;当该用户用水量超过![]() 吨时,超出部分按每吨
吨时,超出部分按每吨![]() 元收取.
元收取.
(1)记某用户在一个收费周期的用水量为![]() 吨,所缴水费为
吨,所缴水费为![]() 元,写出
元,写出![]() 关于
关于![]() 的函数解析式.
的函数解析式.
(2)在某一个收费周期内,若甲、乙两用户所缴水费的和为![]() 元,且甲、乙两用户用水量之比为
元,且甲、乙两用户用水量之比为![]() ,试求出甲、乙两用户在该收费周期内各自的用水量和水费.
,试求出甲、乙两用户在该收费周期内各自的用水量和水费.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】“奶茶妹妹”对某时间段的奶茶销售量及其价格进行调查,统计出售价x元和销售量y杯之间的一组数据如下表所示:
价格x | 5 | 5.5 | 6.5 | 7 |
销售量y | 12 | 10 | 6 | 4 |
通过分析,发现销售量y对奶茶的价格x具有线性相关关系.
(Ⅰ)求销售量y对奶茶的价格x的回归直线方程;
(Ⅱ)欲使销售量为13杯,则价格应定为多少?
注:在回归直线y= ![]() 中,
中,  ,
, ![]() =
= ![]() ﹣
﹣ ![]() .
. ![]() =146.5.
=146.5.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱![]() 与四棱锥
与四棱锥![]() 的组合体中,已知
的组合体中,已知![]() 平面
平面![]() ,四边形
,四边形![]() 是平行四边形,
是平行四边形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,设
,设![]() 是线段
是线段![]() 中点.
中点.

(1)求证: ![]() 平面
平面![]() ;
;
(2)证明:平面![]() 平面
平面![]() ;
;
(3)求四棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某鲜奶店每天以每瓶3元的价格从牧场购进若干瓶鲜牛奶,然后以每瓶7元的价格出售.如果当天卖不完,剩下的鲜牛奶作垃圾处理.
(1)若鲜奶店一天购进30瓶鲜牛奶,求当天的利润![]() (单位:元)关于当天需求量
(单位:元)关于当天需求量![]() (单位:瓶,
(单位:瓶,![]() )的函数解析式;
)的函数解析式;
(2)鲜奶店记录了100天鲜牛奶的日需求量(单位:瓶),绘制出如下的柱形图(例如:日需求量为25瓶时,频数为5);

(i)若该鲜奶店一天购进30瓶鲜牛奶,求这100天的日利润(单位:元)的平均数;
(ii) 若该鲜奶店一天购进30瓶鲜牛奶,以100天记录的各需求量的频率作为各需求量发生的概率,求当天的利润不少于100元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】齐王与田忌赛马,田忌的上等马优于齐王的中等马,劣于齐王的上等马,田忌的中等马优于齐王的下等马,劣于齐王的中等马,田忌的下等马劣于齐王的下等马,现从双方的马匹中随机选一匹进行一场比赛,则田忌马获胜的概率为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
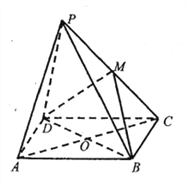
【题目】如图,点![]() 是菱形
是菱形![]() 所在平面外一点,
所在平面外一点, ![]() ,
, ![]() 是等边三角形,
是等边三角形, ![]() ,
, ![]() ,
, ![]() 是
是![]() 的中点.
的中点.
(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求证:平面![]() 平面
平面![]() ;
;
(Ⅲ)求直线![]() 与平面
与平面![]() 的所成角的大小.
的所成角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,函数
,函数![]() 是奇函数.
是奇函数.
(1)判断函数![]() 的奇偶性,并求实数
的奇偶性,并求实数![]() 的值;
的值;
(2)若对任意的![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)设![]() ,若存在
,若存在![]() ,使不等式
,使不等式![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对某校高三年级学生参加社区服务次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数,根据此数据作出了频数与频率的统计表和频率分布直方图.
分组 | 频数 | 频率 |
[10,15) | 10 | 0.25 |
[15,20) | 24 | n |
[20,25) | m | p |
[25,30] | 2 | 0.05 |
合计 | M | 1 |

(1)求出表中M,p及图中a的值;
(2)若该校高三学生有240人,试估计该校高三学生参加社区服务的次数在区间[10,15)内的人数;
(3)估计这次学生参加社区服务人数的众数、中位数以及平均数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com