
(I)求证:BD⊥A1C;
(II)求二面角A 1-BD-C 1的大小;
(III)求异面直线 AD与 BC 1所成角的大小.

(16)解法一:

(I)在直四棱柱ABCD-A1B1C1D1中,
∵AA1⊥底面ABCD.
∴ AC是A1C在平面ABCD上的射影.
∵BD⊥AC.
∴ BD⊥A1C;
(II)连结A1E,C1E,A1C1.
与(I)同理可证BD⊥A1E,BD⊥C1E,
∴ ∠A1EC1为二面角A1-BD-C1的平面角.
∵ AD⊥DC,
∴ ∠A1D1C1=∠ADC=90°,
又A1D1=AD=2,D1C1= DC=2![]() ,AA1=
,AA1=![]() 且 AC⊥BD,
且 AC⊥BD,
∴ A1C1=4,AE=1,EC=3,
∴ A1E=2,C1E=2![]() ,
,
在△A1EC1中,A1C12=A1E2+C1E2,
∴ ∠A1EC1=90°,
即二面角A1-BD-C1的大小为90°.
(III)过B作 BF//AD交 AC于 F,连结FC1,
则∠C1BF就是AD与BC1所成的角.
∵AB=AD=2, BD⊥AC,AE=1,
∴BF=2,EF=1,FC=2,BC=DC,
∴ FC1=![]() ,BC1=
,BC1=![]() ,
,
在△BFC1 中,cos∠C1BF=![]()
∴ ∠C1BF= ![]()
即异面直线AD与BC1所成角的大小为![]() .
.
解法二:
(Ⅰ)同解法一。
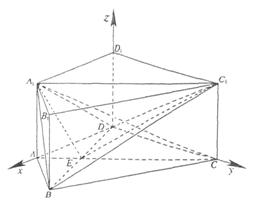
(Ⅱ)如图,以D为坐标原点,DA,DC,DD1所在直线分别为x轴,y轴,z轴,建立空间直角坐标系。
连结A1E,C1E,A1C1
与(Ⅰ)同理可证,BD⊥A1E,BD⊥C1E ,
∴∠A1EC1为二面角A1-BD-C1的平面角。
由A1(2,0,![]() ),C1(0,2
),C1(0,2![]() ,
,![]() ),
),
E(![]() ,0),
,0),
得![]() =(
=(![]() ),
),![]() =(-
=(-![]() )
)
∴![]() ·
·![]() =
=![]()
![]() +3=0
+3=0
∴![]() ⊥
⊥![]() ,即EA1⊥EC1
,即EA1⊥EC1
∴二面角A1-BD-C1的大小为90°
(Ⅲ)如图,由D(0,0,0),A(2,0,0),C1(0,2![]() ,
,![]() ),B(3,
),B(3, ![]() ,0)
,0)
得![]() =(-2,0,0),
=(-2,0,0),![]() =(-3,
=(-3, ![]() ,
,![]() )
)
∴![]() ·
·![]() =6,|
=6,|![]() |=2,|
|=2,|![]() |=
|=![]() ,
,
∴cos(![]() ,
,![]() )=
)= =
=![]() =
=![]() ,
,
∴异面直线AD与BC1所成的角大小为arccos![]() .
.
解法三:
(Ⅰ)同解法一。
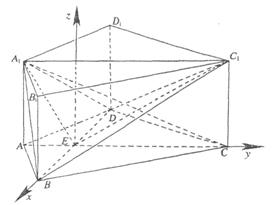
(Ⅱ)如图,建立空间直角坐标系,坐标原点为E。
连结A1E,C1E,A1C1
与(Ⅰ)同理可证,BD⊥A1E,BD⊥C1E,
∴∠A1EC1为二面角A1-BD-C1的平面角。
由E(0,0,0),
A1(0,-1,![]() ),
),
C1(0,3,![]() ),
),
得![]() ,
,![]() =(0,3,
=(0,3,![]() )。
)。
∵![]() ·
·![]() =-3+3=0
=-3+3=0
∴![]() ⊥
⊥![]() ,即EA1⊥EC1
,即EA1⊥EC1
∴二面角A1-BD-C1的大小为90°
(Ⅲ)如图,由A(0,-1,0),D(-![]() ,0,0),B(
,0,0),B(![]() ,0,0),C1(0,3,
,0,0),C1(0,3,![]() )
)
得![]() =(-
=(-![]() ,1,0),
,1,0),![]() =(-
=(-![]() ,3,
,3,![]() )。
)。
∵![]() ·
·![]() =3+3=6,|
=3+3=6,|![]() |=2,|
|=2,|![]() |=
|=![]()
∴cos<![]() ,
,![]() >=
>=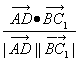 =
=![]() =
=![]() ,
,
∴异面直线AD与BC1所成的角大小为arccos![]() .
.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:高中数学 来源: 题型:
 16、16、如图,在正方体ABCD-A1B1C1D1中,M、N分别是棱C1D1、C1C的中点.以下四个结论:
16、16、如图,在正方体ABCD-A1B1C1D1中,M、N分别是棱C1D1、C1C的中点.以下四个结论:查看答案和解析>>
科目:高中数学 来源: 题型:
(上海卷理16文16)如图,在棱长为2的正方体
ABCD-A1B1C1D1中,E是BC1的中点,求直线DE与平面
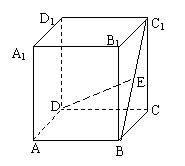 ABCD所成角的大小(结果用反三角函数表示)
ABCD所成角的大小(结果用反三角函数表示)
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江苏省高三第一学期第二次阶段考试数学 题型:解答题
(本小题满分16分)如图,在平面直角坐标系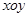 中,已知
中,已知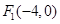 ,
, ,
,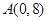 ,直线
,直线 与线段
与线段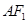 、
、 分别交于点
分别交于点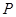 、
、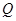 .
.
(Ⅰ)当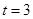 时,求以
时,求以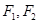 为焦点,且过
为焦点,且过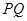 中点的椭圆的标准方程;
中点的椭圆的标准方程;
(Ⅱ)过点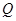 作直线
作直线 ∥
∥ 交
交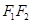 于点
于点 ,记
,记 的外接圆为圆
的外接圆为圆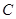 .
.
①
求证:圆心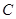 在定直线
在定直线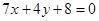 上;
上;
②
圆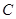 是否恒过异于点
是否恒过异于点 的一个定点?若过,求出该点的坐标;若不过,请说明理由.
的一个定点?若过,求出该点的坐标;若不过,请说明理由.
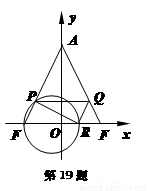
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江苏省南京市高三下学期入学测试数学试卷 题型:解答题
(本小题满分16分)如图,在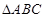 中,
中,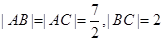 ,以
,以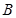 、
、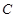 为焦点的椭圆恰好过
为焦点的椭圆恰好过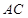 的中点
的中点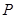 .
.
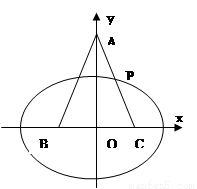
(1)求椭圆的标准方程;
(2)过椭圆的右顶点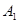 作直线
作直线 与圆
与圆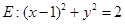 相交于
相交于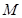 、
、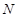 两点,试探究点
两点,试探究点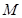 、
、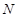 能将圆
能将圆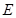 分割成弧长比值为
分割成弧长比值为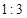 的两段弧吗?若能,求出直线
的两段弧吗?若能,求出直线 的方程;若不能,请说明理由.
的方程;若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com