
【题目】已知函数 ![]() .
.
(1)当 ![]() 时,求曲线
时,求曲线 ![]() 在点
在点 ![]() 处的切线方程;
处的切线方程;
(2)求 ![]() 的单调区间.
的单调区间.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2x-1,![]() (a∈R),若对任意x1∈[1,+∞),总存在x2∈R,使f(x1)=g(x2),则实数a的取值范围是()
(a∈R),若对任意x1∈[1,+∞),总存在x2∈R,使f(x1)=g(x2),则实数a的取值范围是()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某石化集团获得了某地深海油田区块的开采权.集团在该地区随机初步勘探了部分几口井.取得了地质资料,进入全面勘探时期后.集团按网络点来布置井位进行全面勘探.由于勘探一口井的费用很高.如果新设计的井位与原有井位重合或接近.便利用旧并的地质资料.不必打这日新并,以节约勘探费与用,勘探初期数据资料见如表:
井号 |
|
|
|
|
|
|
坐标 |
|
|
|
|
|
|
钻探深度 |
|
|
|
|
|
|
出油量 |
|
|
|
|
|
|
(参考公式和计算结果: ,
,![]() ,
,![]() ,
,![]() ).
).
(![]() )
)![]() 号旧井位置线性分布,借助前
号旧井位置线性分布,借助前![]() 组数据求得回归直线方程为
组数据求得回归直线方程为![]() ,求
,求![]() 的值.
的值.
(![]() )现准备勘探新井
)现准备勘探新井![]() ,若通过
,若通过![]() ,
,![]() ,
,![]() ,
,![]() 号井计算出的
号井计算出的![]() ,
,![]() 的值(
的值(![]() ,
,![]() 精确到
精确到![]() )相比于(
)相比于(![]() )中的
)中的![]() ,
,![]() ,值之差不超过
,值之差不超过![]() .则使用位置最接近的已有旧井
.则使用位置最接近的已有旧井![]() .否则在新位置打开,请判断可否使用旧井?
.否则在新位置打开,请判断可否使用旧井?
(![]() )设出油量与勘探深度的比值
)设出油量与勘探深度的比值![]() 不低于
不低于![]() 的勘探井称为优质井,那么在原有
的勘探井称为优质井,那么在原有![]() 口井中任意勘探
口井中任意勘探![]() 口井,求勘探优质井数
口井,求勘探优质井数![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x,g(x)=x-4,则下列结论正确的是( )
A.若h(x)=f(x)g(x),则函数h(x)的最小值为4
B.若h(x)=f(x)|g(x)|,则函数h(x)的值域为R
C.若h(x)=|f(x)|-|g(x)|,则函数h(x)有且仅有一个零点
D.若h(x)=|f(x)|-|g(x)|,则|h(x)|≤4恒成立
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法:①对于独立性检验,![]() 的值越大,说明两事件相关程度越大,②以模型
的值越大,说明两事件相关程度越大,②以模型![]() 去拟合一组数据时,为了求出回归方程,设
去拟合一组数据时,为了求出回归方程,设![]() ,将其变换后得到线性方程
,将其变换后得到线性方程![]() ,则
,则![]() 的值分别是
的值分别是![]() 和
和![]() ,③某中学有高一学生400人,高二学生300人,高三学生200人,学校团委欲用分层抽样的方法抽取18名学生进行问卷调查,则高一学生被抽到的概率最大,④通过回归直线
,③某中学有高一学生400人,高二学生300人,高三学生200人,学校团委欲用分层抽样的方法抽取18名学生进行问卷调查,则高一学生被抽到的概率最大,④通过回归直线![]() =
=![]()
![]() +
+![]() 及回归系数
及回归系数![]() ,可以精确反映变量的取值和变化趋势,其中正确的个数是
,可以精确反映变量的取值和变化趋势,其中正确的个数是
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为回馈顾客,新华都购物商场拟通过摸球兑奖的方式对500位顾客进行奖励,规定:每位顾客从一个装有4个标有面值的球的袋中一次性随机摸出2个球(球的大小、形状一模一样),球上所标的面值之和为该顾客所获的奖励额.
(1)若袋中所装的4个球中有1个所标的面值为40元,其余3个所标的面值均为20元,求顾客所获的奖励额![]() 的分布列及数学期望;
的分布列及数学期望;
(2)商场对奖励总额的预算是30000元,并规定袋中的4个球由标有面值为20元和40元的两种球共同组成,或标有面值为15元和45元的两种球共同组成.为了使顾客得到的奖励总额尽可能符合商场的预算且每位顾客所获的奖励额相对均衡.请对袋中的4个球的面值给出一个合适的设计,并说明理由.
提示:袋中的4个球由标有面值为a元和b元的两种球共同组成,即袋中的4个球所标的面值“既有a元又有b元”.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,圆O:![]() ,
,![]() ,
,![]() ,D为圆O上任意一点,过D作圆O的切线分别交直线
,D为圆O上任意一点,过D作圆O的切线分别交直线![]() 和
和![]() 于E,F两点,连AF,BE交于点G,若点G形成的轨迹为曲线C.
于E,F两点,连AF,BE交于点G,若点G形成的轨迹为曲线C.
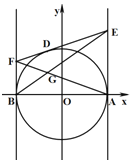
![]() 记AF,BE斜率分别为
记AF,BE斜率分别为![]() ,
,![]() ,求
,求![]() 的值并求曲线C的方程;
的值并求曲线C的方程;
![]() 设直线l:
设直线l:![]() 与曲线C有两个不同的交点P,Q,与直线
与曲线C有两个不同的交点P,Q,与直线![]() 交于点S,与直线
交于点S,与直线![]() 交于点T,求
交于点T,求![]() 的面积与
的面积与![]() 面积的比值
面积的比值![]() 的最大值及取得最大值时m的值.
的最大值及取得最大值时m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中错误的是__________(填序号)
①命题“![]() ,有
,有![]() ”的否定是“
”的否定是“![]() ”,有
”,有![]() ”;
”;
②已知![]() ,
, ![]() ,
, ![]() ,则
,则![]() 的最小值为
的最小值为![]() ;
;
③设![]() ,命题“若
,命题“若![]() ,则
,则![]() ”的否命题是真命题;
”的否命题是真命题;
④已知![]() ,
, ![]() ,若命题
,若命题![]() 为真命题,则
为真命题,则![]() 的取值范围是
的取值范围是![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com