
【题目】如图所示,在四边形ABCD中,AC=CD=![]() AB=1,
AB=1, ![]() ,sin∠BCD=
,sin∠BCD=![]() .
.
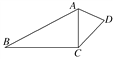
(1)求BC边的长;
(2)求四边形ABCD的面积.
【答案】(1) ![]() (2)
(2) ![]()
【解析】 试题分析:(1)先根据向量数量积求∠BAC,再根据余弦定理求BC边的长;(2)四边形ABCD的面积等于两个三角形面积之和,而△ABC为直角三角形,可得其面积;根据∠BCD=∠ACB+∠ACD=90°+∠ACD,所以先由sin∠BCD=![]() 求sin∠ACD,再根据三角形面积公式求S△ACD,最后相加得四边形ABCD的面积
求sin∠ACD,再根据三角形面积公式求S△ACD,最后相加得四边形ABCD的面积
试题解析:(1)∵AC=CD=![]() AB=1,∴
AB=1,∴![]() =2cos∠BAC=1.
=2cos∠BAC=1.
∴cos∠BAC=![]() ,∴∠BAC=60°.
,∴∠BAC=60°.
在△ABC中,由余弦定理,有
BC2=AB2+AC2-2AB·AC·cos∠BAC=22+12-2×2×1×![]() =3,∴BC=
=3,∴BC=![]() .
.
(2)由(1)知,在△ABC中,有AB2=BC2+AC2.∴△ABC为直角三角形,且∠ACB=90°.
∴S△ABC=![]() BC·AC=
BC·AC=![]()
又∠BCD=∠ACB+∠ACD=90°+∠ACD,sin∠BCD=,∴cos∠ACD=.
从而sin∠ACD=![]() .
.
∴S△ACD=![]() AC·CD·sin∠ACD=
AC·CD·sin∠ACD=![]() ×1×1×
×1×1×![]() =.
=.
∴S四边形ABCD=S△ABC+S△ACD=+=![]() .
.


科目:高中数学 来源: 题型:
【题目】在锐角三角形中,边a、b是方程x2﹣2 ![]() x+2=0的两根,角A、B满足:2sin(A+B)﹣
x+2=0的两根,角A、B满足:2sin(A+B)﹣ ![]() =0,求角C的度数,边c的长度及△ABC的面积.
=0,求角C的度数,边c的长度及△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 且满足Sn=2an﹣2.若数列{bn}满足bn=10﹣log2an , 则是数列{bn}的前n项和取最大值时n的值为( )
A.8
B.10
C.8或9
D.9或10
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市为了了解今年高中毕业生的体能状况,从某校高中毕业班中抽取一个班进行铅球测试,成绩在8.0米(精确到0.1米)以上的为合格.数据分成6组画出频率分布直方图的一部分(如图),已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30 .第6小组的频数是7.
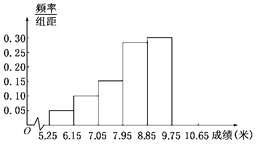
(I)求这次铅球测试成绩合格的人数;
(II)若参加测试的学生中9人成绩优秀,现要从成绩优秀的学生中,随机选出2人参加“毕业运动会”,已知学生![]() 、
、![]() 的成绩均为优秀,求两人
的成绩均为优秀,求两人![]() 、
、![]() 至少有1人入选的概率.
至少有1人入选的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在四边形ABCD中,AB⊥DA,CE= ![]() ,∠ADC=
,∠ADC= ![]() ;E为AD边上一点,DE=1,EA=2,∠BEC=
;E为AD边上一点,DE=1,EA=2,∠BEC= ![]()
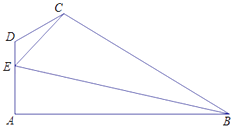
(1)求sin∠CED的值;
(2)求BE的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某食品店为了了解气温对销售量的影响,随机记录了该店1月份中5天的日销售量![]() (单位:千克)与该地当日最低气温
(单位:千克)与该地当日最低气温![]() (单位:
(单位: ![]() )的数据,如下表:
)的数据,如下表:
x | 2 | 5 | 8 | 9 | 11 |
y | 12 | 10 | 8 | 8 | 7 |
(1)求出![]() 与
与![]() 的回归方程
的回归方程![]() ;
;
(2)判断![]() 与
与![]() 之间是正相关还是负相关;若该地1月份某天的最低气温为
之间是正相关还是负相关;若该地1月份某天的最低气温为![]() ,请用所求回归方程预测该店当日的销售量;
,请用所求回归方程预测该店当日的销售量;
(3)设该地1月份的日最低气温![]() ~
~![]() ,其中
,其中![]() 近似为样本平均数
近似为样本平均数![]() ,
, ![]() 近似为样本方差
近似为样本方差![]() ,求
,求![]() .
.
附:①回归方程![]() 中,
中, 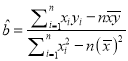 ,
, ![]() .
.
②![]() ,
, ![]() ,若
,若![]() ~
~![]() ,则
,则![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“累积净化量![]() ”是空气净化器质量的一个重要衡量指标,它是指空气净化从开始使用到净化效率为50%时对颗粒物的累积净化量,以克表示,根据
”是空气净化器质量的一个重要衡量指标,它是指空气净化从开始使用到净化效率为50%时对颗粒物的累积净化量,以克表示,根据![]() 《空气净化器》国家标准,对空气净化器的累计净化量
《空气净化器》国家标准,对空气净化器的累计净化量![]() 有如下等级划分:
有如下等级划分:
累积净化量(克) |
|
|
| 12以上 |
等级 |
|
|
|
|
为了了解一批空气净化器(共5000台)的质量,随机抽取![]() 台机器作为样本进行估计,已知这
台机器作为样本进行估计,已知这![]() 台机器的累积净化量都分布在区间
台机器的累积净化量都分布在区间![]() 中,按照
中,按照![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 均匀分组,其中累积净化量在
均匀分组,其中累积净化量在![]() 的所有数据有:4.5,4.6,5.2,5.3,5.7和5.9,并绘制了频率分布直方图,如图所示:
的所有数据有:4.5,4.6,5.2,5.3,5.7和5.9,并绘制了频率分布直方图,如图所示:
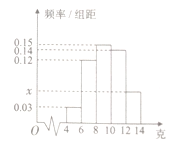
(1)求![]() 的值及频率分布直方图中
的值及频率分布直方图中![]() 的值;
的值;
(2)以样本估计总体,试估计这批空气净化器(共5000台)中等级为![]() 的空气净化器有多少台?
的空气净化器有多少台?
(3)从累积净化量在![]() 的样本中随机抽取2台,求恰好有1台等级为
的样本中随机抽取2台,求恰好有1台等级为![]() 的概率.
的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com