
【题目】数列 ![]() 满足
满足 ![]() ,且
,且 ![]() .
.
(1)写出 ![]() 的前3项,并猜想其通项公式;
的前3项,并猜想其通项公式;
(2)用数学归纳法证明你的猜想.
【答案】
(1)解: ![]() ,猜想
,猜想 ![]() ;(2)①验证
;(2)①验证 ![]() 时成立; ②假设
时成立; ②假设 ![]() 时,猜想成立,即有
时,猜想成立,即有 ![]() ,由
,由 ![]() ,,及
,,及 ![]() ,证得
,证得 ![]() 时成立,故命题成立.
时成立,故命题成立.
(2)解:①当 ![]() 时,
时, ![]() 成立;
成立;
②假设 ![]() 时,猜想成立,即有
时,猜想成立,即有 ![]() ,
,
由 ![]() ,,及
,,及 ![]() ,
,
得 ![]() ,即当
,即当 ![]() 时猜想成立,
时猜想成立,
由①②可知, ![]() 对一切正整数
对一切正整数 ![]() 均成立.
均成立.
【解析】(1)将n=1,n=2分别代入递推关系式中即可求出a2,a3,通过观察前3项的规律可发现数列{an}是一个等差数列,根据等差数列的通项公式an=a1+(n-1)d即可写出an并验证;(2)验证当n=1时猜想成立,假设当n=k时猜想成立,证明当n=k+1时猜想成立.
【考点精析】关于本题考查的数列的通项公式,需要了解如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能得出正确答案.


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:高中数学 来源: 题型:
【题目】把函数 ![]() 的图象上每个点的横坐标扩大到原来的4倍,再向左平移
的图象上每个点的横坐标扩大到原来的4倍,再向左平移 ![]() ,得到函数g(x)的图象,则函数g(x)的一个单调递减区间为( )
,得到函数g(x)的图象,则函数g(x)的一个单调递减区间为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某渔船在航行中不幸遇险,发出呼叫信号,我海军舰艇在![]() 处获悉后,立即测出该渔船在方位角(从指北方向顺时针转到目标方向线的水平角)为
处获悉后,立即测出该渔船在方位角(从指北方向顺时针转到目标方向线的水平角)为![]() ,距离为15海里的
,距离为15海里的![]() 处,并测得渔船正沿方位角为
处,并测得渔船正沿方位角为![]() 的方向,以15海里/小时的速度向小岛
的方向,以15海里/小时的速度向小岛![]() 靠拢,我海军舰艇立即以
靠拢,我海军舰艇立即以![]() 海里/小时的速度前去营救,求舰艇靠近渔船所需的最少时间和舰艇的航向.
海里/小时的速度前去营救,求舰艇靠近渔船所需的最少时间和舰艇的航向.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直三棱柱ABC﹣A1B1C1的底面为正三角形,E,F分别是A1C1 , B1C1上的点,且满足A1E=EC1 , B1F=3FC1 . 
(1)求证:平面AEF⊥平面BB1C1C;
(2)设直三棱柱ABC﹣A1B1C1的棱长均相等,求二面角C1﹣AE﹣B的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商店对新引进的商品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:
定价 | 9 | 9.2 | 9.4 | 9.6 | 9.8 | 10 |
销量 | 100 | 94 | 93 | 90 | 85 | 78 |
(1)求回归直线方程![]() ;
;
(2)假设今后销售依然服从(Ⅰ)中的关系,且该商品金价为每件5元,为获得最大利润,商店应该如何定价?(利润=销售收入-成本)
参考公式:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种水果的单个质量在500g以上视为特等品.随机抽取1000个该水果,结果有50个特等品.将这50个水果的质量数据分组,得到下边的频率分布表.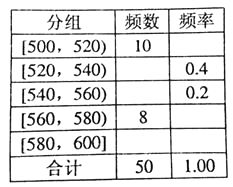
(1)估计该水果的质量不少于560g的概率;
(2)若在某批水果的检测中,发现有15个特等品,据此估计该批水果中没有达到特等品的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从参加某次知识竞赛的同学中,选取60名同学将其成绩(百分制,均为整数)分成![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 六组后,得到部分频率分布直方图(如图),观察图形中的信息,回答下列问题:
六组后,得到部分频率分布直方图(如图),观察图形中的信息,回答下列问题:

(1)求分数![]() 内的频率,并补全这个频率分布直方图;
内的频率,并补全这个频率分布直方图;
(2)从频率分布直方图中,估计本次考试成绩的中位数;
(3)若从第1组和第6组两组学生中,随机抽取2人,求所抽取2人成绩之差的绝对值大于10的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】拖延症总是表现在各种小事上,但日积月累,特别影响个人发展.某校的一个社会实践调查小组,在对该校学生进行“是否有明显拖延症”的调查中,随机发放了110份问卷.对收回的100份有效问卷进行统计,得到如下 ![]() 列联表:
列联表:
(1)按女生是否有明显拖延症进行分层,已经从40份女生问卷中抽取了8份问卷,现从这8份问卷中再随机抽取3份,并记其中无明显拖延症的问卷的份数为 ![]() ,试求随机变量
,试求随机变量 ![]() 的分布列和数学期望;
的分布列和数学期望;
(2)若在犯错误的概率不超过 ![]() 的前提下认为无明显拖延症与性别有关,那么根据临界值表,最精确的
的前提下认为无明显拖延症与性别有关,那么根据临界值表,最精确的 ![]() 的值应为多少?请说明理由.附:独立性检验统计量
的值应为多少?请说明理由.附:独立性检验统计量 ![]() ,其中
,其中 ![]() .
.
独立性检验临界值表:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com