
【题目】已知函数f(x)=(x+m)lnx,曲线y=f(x)在x=e(e为自然对数的底数)处得到切线与圆x2+y2=5在点(2,﹣1)处的切线平行.
(1)证明: ![]() ;
;
(2)若不等式(ax+1)(x﹣1)<(a+1)lnx在x∈(0,1)上恒成立,求实数a的取值范围.
【答案】
(1)证明:∵f(x)=(x+m)lnx,
∴f′(x)=lnx+ ![]() ,
,
易知圆x2+y2=5在点(2,﹣1)处的切线方程是2x﹣y=5,
由题意得f′(e)=2,即lne+ ![]() =2,解得:m=0,
=2,解得:m=0,
∴f(x)=xlnx,f′(x)=lnx+1,
令f′(x)=0,解得:x= ![]() ,
,
x∈(0, ![]() )时,f′(x)<0,
)时,f′(x)<0,
故f(x)在(0, ![]() )递减,
)递减,
x∈( ![]() ,+∞)时,f′(x)>0,
,+∞)时,f′(x)>0,
故f(x)在( ![]() ,+∞)递增,
,+∞)递增,
故f(x)在x= ![]() 处取极小值,也是最小值,最小值是f(
处取极小值,也是最小值,最小值是f( ![]() )=﹣
)=﹣ ![]() ,
,
又﹣ ![]() >﹣
>﹣ ![]() ,故f(x)>﹣
,故f(x)>﹣ ![]()
(2)解:若不等式(ax+1)(x﹣1)<(a+1)lnx在x∈(0,1)上恒成立,
则(a+1)lnx+ ![]() ﹣ax+a﹣1>0在x∈(0,1)上恒成立,
﹣ax+a﹣1>0在x∈(0,1)上恒成立,
设h(x)=(a+1)lnx+ ![]() ﹣ax+a﹣1,x∈(0,+∞),
﹣ax+a﹣1,x∈(0,+∞),
则h′(x)= ![]() ,
,
①a≤0时,h′(x)<0在(0,1)恒成立,
故h(x)在(0,1)递减,又h(1)=0,
故x∈(0,1)时,总有h(x)>0,符合题意;
②a>1时,令h′(x)=0,解得:x= ![]() 或x=1,
或x=1,
易知h(x)在(0, ![]() )递减,在(
)递减,在( ![]() ,1)递增,又h(1)=0,
,1)递增,又h(1)=0,
故x∈( ![]() ,1)时,总有h(x)<0,不符合题意;
,1)时,总有h(x)<0,不符合题意;
③0<a≤1时,h′(x)<0在(0,1)恒成立,
故h(x)在(0,1)递减,又h(1)=0,
故x∈(0,1)时,总有h(x)>0,符合题意;
综上,a的范围是(﹣∞,1]
【解析】(1)求出函数的导数,求出m的值,解关于导函数的不等式,求出函数的单调区间,从而求出函数的最小值即可;(2)问题转化为(a+1)lnx+ ![]() ﹣ax+a﹣1>0在x∈(0,1)上恒成立,设h(x)=(a+1)lnx+
﹣ax+a﹣1>0在x∈(0,1)上恒成立,设h(x)=(a+1)lnx+ ![]() ﹣ax+a﹣1,x∈(0,+∞),根据函数的单调性求出a的范围即可.
﹣ax+a﹣1,x∈(0,+∞),根据函数的单调性求出a的范围即可.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,且满足acosB=bcosA.
(1)判断△ABC的形状;
(2)求sin(2A+ ![]() )﹣2cos2B的取值范围.
)﹣2cos2B的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知F1 , F2为椭圆E的左右焦点,点P(1, ![]() )为其上一点,且有|PF1|+|PF2|=4
)为其上一点,且有|PF1|+|PF2|=4
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)过F1的直线l1与椭圆E交于A,B两点,过F2与l1平行的直线l2与椭圆E交于C,D两点,求四边形ABCD的面积SABCD的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线C1的参数方程为 ![]() (φ为参数),以原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=4sinθ
(φ为参数),以原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=4sinθ
(Ⅰ)求曲线C1的普通方程和C2的直角坐标方程;
(Ⅱ)已知曲线C3的极坐标方程为θ=α,0<α<π,ρ∈R,点A是曲线C3与C1的交点,点B是曲线C3与C2的交点,且A,B均异于原点O,且|AB|=4 ![]() ,求实数a的值.
,求实数a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两位打字员在两台电脑上各自输入A,B两种类型的文件的部分文字才能使这两类文件成为成品.已知A文件需要甲输入0.5小时,乙输入0.2小时;B文件需要甲输入0.3小时,乙输入0.6小时.在一个工作日中,甲至多只能输入6小时,乙至多只能输入8小时,A文件每份的利润为60元,B文件每份的利润为80元,则甲、乙两位打字员在一个工作日内获得的最大利润是元.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分8分)某班50名学生在一次数学测试中,成绩全部介于50与100之间,将测试结果按如下方式分成五组:第一组[50,60),第二组[60,70),…,第五组[90,100].如图所示是按上述分组方法得到的频率分布直方图.
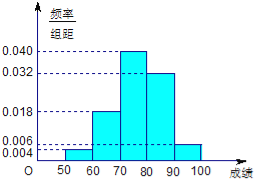
(Ⅰ)若成绩大于或等于60且小于80,认为合格,求该班在这次数学测试中成绩合格的人数;
(Ⅱ)从测试成绩在[50,60)∪[90,100]内的所有学生中随机抽取两名同学,设其测试成绩分别为m、n,求事件“|m﹣n|>10”概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知O为坐标原点,椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,离心率
,离心率![]() ,椭圆
,椭圆![]() 上的点到焦点
上的点到焦点![]() 的最短距离为
的最短距离为![]() .
.
(1)求椭圆C的标准方程;
(2)设T为直线![]() 上任意一点,过
上任意一点,过![]() 的直线交椭圆C于点P,Q,且为抛物线
的直线交椭圆C于点P,Q,且为抛物线![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(1﹣m)lnx+ ![]() ﹣x,m∈R且m≠0.
﹣x,m∈R且m≠0.
(Ⅰ)当m=2时,令g(x)=f(x)+log2(3k﹣1),k为常数,求函数y=g(x)的零点的个数;
(Ⅱ)若不等式f(x)>1﹣ ![]() 在x∈[1,+∞)上恒成立,求实数m的取值范围.
在x∈[1,+∞)上恒成立,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com