
【题目】设已知抛物线C:y2=2px的焦点为F1 , 过F1的直线l与曲线C相交于M,N两点.
(1)若直线l的倾斜角为60°,且|MN|= ![]() ,求p;
,求p;
(2)若p=2,椭圆 ![]() +y2=1上两个点P,Q,满足:P,Q,F1三点共线且PQ⊥MN,求四边形PMQN的面积的最小值.
+y2=1上两个点P,Q,满足:P,Q,F1三点共线且PQ⊥MN,求四边形PMQN的面积的最小值.
【答案】
(1)解:直线l的方程为y= ![]() (x﹣
(x﹣ ![]() ),代入抛物线方程,整理可得
),代入抛物线方程,整理可得 ![]() =0,
=0,
∴xN+xM= ![]() ,
,
∵|MN|= ![]() ,
,
∴ ![]() +p=
+p= ![]() ,∴p=2;
,∴p=2;
(2)解:当直线MN斜率不存在时,直线PQ斜率为0,此时|MN|=4,|PQ|=2 ![]() ,SPMQN=4
,SPMQN=4 ![]() .
.
当直线MN斜率存在时,设方程为y=k(x﹣1)(k≠0),代入抛物线可得k2x2﹣(2k2+4)x+k2=0,
∴xM+xN= ![]() +2,
+2,
∴|MN|= ![]() +4
+4
由PQ⊥MN,可设PQ的方程y=﹣ ![]() (x﹣1),代入椭圆方程得(k2+2)x2﹣4x+2﹣2k2=0,
(x﹣1),代入椭圆方程得(k2+2)x2﹣4x+2﹣2k2=0,
∴xP+xQ= ![]() ,xPxQ=
,xPxQ= ![]() ,
,
∴PQ|= ![]()
![]() =
= ![]() ,
,
∴S= ![]() ,
,
令t=1+k2(t>1),S= ![]() =4
=4 ![]() (1+
(1+ ![]() )>4
)>4 ![]() ,
,
∴四边形PMQN的面积的最小值为4 ![]() .
.
【解析】(1)直线l的方程为y= ![]() (x﹣
(x﹣ ![]() ),代入抛物线方程,利用弦长公式,求p;(2)分类讨论,求出弦长,表示面积,即可得出结论.
),代入抛物线方程,利用弦长公式,求p;(2)分类讨论,求出弦长,表示面积,即可得出结论.


 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:高中数学 来源: 题型:
【题目】《孙子算经》是我国古代的数学著作,其卷下中有类似如下的问题:“今有方物一束,外周一匝有四十枚,问积几何?”如右图是解决该问 题的程序框图,若设每层外周枚数为a,则输出的结果为( )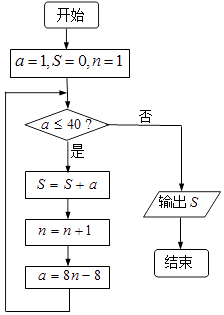
A.81
B.74
C.121
D.169
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某重点中学为了解高一年级学生身体发育情况,对全校700名高一年级学生按性别进行分层抽样检查,测得身高(单位:cm)频数分布表如表1、表2. 表1:男生身高频数分布表
身高(cm) | [160,165) | [165,170) | [170,175) | [175,180) | [180,185) | [185,190) |
频数 | 2 | 5 | 14 | 13 | 4 | 2 |
表2:女生身高频数分布表
身高(cm) | [150,155) | [155,160) | [160,165) | [165,170) | [170,175) | [175,180) |
频数 | 1 | 7 | 12 | 6 | 3 | 1 |
(1)求该校高一女生的人数;
(2)估计该校学生身高在[165,180)的概率;
(3)以样本频率为概率,现从高一年级的男生和女生中分别选出1人,设X表示身高在[165,180)学生的人数,求X的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的内角A、B、C的对边分别为a、b、c,已知△ABC的面积为accosB,BC的中点为D. (Ⅰ) 求cosB的值;
(Ⅱ) 若c=2,asinA=5csinC,求AD的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个几何体的三视图如图所示,则这个几何体的表面积为( ) 
A.24+8 ![]() +8
+8 ![]()
B.20+8 ![]() +4
+4 ![]() ??
??
C.20+8 ![]() +4
+4 ![]()
D.20+4 ![]() +4
+4 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题的叙述:
①若p:x>0,x2﹣x+1>0,则¬p:x0≤0,x02﹣x0+1≤0;
②三角形三边的比是3:5:7,则最大内角为 ![]() π;
π;
③若 ![]()
![]() =
= ![]()
![]() ,则
,则 ![]() =
= ![]() ;
;
④ac2<bc2是a<b的充分不必要条件,
其中真命题的个数为( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在公差不为零的等差数列{an}中,已知a2=3,且a1、a3、a7成等比数列.
(1)求数列{an}的通项公式;
(2)设数列{an}的前n项和为Sn , 记bn= ![]() ,求数列{bn}的前n项和Tn .
,求数列{bn}的前n项和Tn .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com