
【题目】已知关于某设备的使用年限![]() 与所支出的维修费用
与所支出的维修费用![]() (万元),有如下统计资料:
(万元),有如下统计资料:
设![]() 对
对![]() 呈线性相关关系,试求:
呈线性相关关系,试求:

(1)线性回归方程![]() 的回归系数
的回归系数![]() ;
;
(2)估计使用年限为10年时,维修费用是多少?
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)根据表中的数据,得到![]() ,利用最小二乘法求得
,利用最小二乘法求得![]() ,求得
,求得![]() 的值,得到回归方程;(2)根据(1)的结果,写出回归直线方程,代入
的值,得到回归方程;(2)根据(1)的结果,写出回归直线方程,代入![]() ,即可得到使用年限为
,即可得到使用年限为![]() 年时,维修费用.
年时,维修费用.
试题解析:(1)根据y对x呈线性相关关系,相关信息列表知
=(2+3+4+5+6)÷5=4,=(2.5+3.5+5.5+6.5+7.0)÷5=5
代入公式计算得:b=![]() =
=![]() =1.23;
=1.23;
a=-b=5-1.23×4=0.08,
(2)根据(1)的结果,写出回归直线方程为y=1.23x+0.08,
当x=10年时,y=1.23×10+0.08=12.3+0.08=12.38(万元)
即估计使用10年时,维修费用是12.38万元.


科目:高中数学 来源: 题型:
【题目】已知平面五边形![]() 是轴对称图形(如图1),BC为对称轴,AD⊥CD,AD=AB=1,
是轴对称图形(如图1),BC为对称轴,AD⊥CD,AD=AB=1,![]() ,将此五边形沿BC折叠,使平面ABCD⊥平面BCEF,得到如图2所示的空间图形,对此空间图形解答下列问题.
,将此五边形沿BC折叠,使平面ABCD⊥平面BCEF,得到如图2所示的空间图形,对此空间图形解答下列问题.
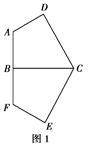
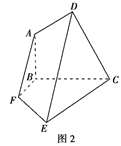
(1)证明:AF∥平面DEC;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 在它的某一个周期内的单调减区间是
在它的某一个周期内的单调减区间是![]() .
.
(1)求![]() 的解析式;
的解析式;
(2)将![]() 的图象先向右平移
的图象先向右平移![]() 个单位,再将图象上所有点的横坐标变为原来的
个单位,再将图象上所有点的横坐标变为原来的![]() 倍(纵坐标不变),所得到的图象对应的函数记为
倍(纵坐标不变),所得到的图象对应的函数记为![]() ,若对于任意的
,若对于任意的![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个命题:
①函数![]() 的图像过定点
的图像过定点![]() ;
;
②已知函数![]() 是定义在
是定义在![]() 上的偶函数,当
上的偶函数,当![]() 时,
时,![]() ,则
,则![]() 的解析式为
的解析式为![]() ;
;
③函数![]() 的图像可由函数
的图像可由函数![]() 图像向右平移一个单位得到;
图像向右平移一个单位得到;
④函数![]() 图像上的点到
图像上的点到![]() 距离的最小值是
距离的最小值是![]() .
.
其中所有正确命题的序号是_____________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】宜昌一中江南新校区拟建一个扇环形状的花坛(如图所示),按设计要求扇环的周长为30米,其中大圆弧所在圆的半径为10米,设小圆弧所在圆的半径为![]() 米,圆心角
米,圆心角![]() (弧度).
(弧度).
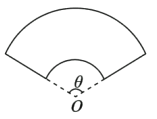
(1)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)已知对花坛的边缘(实线部分)进行装饰时,直线部分的装饰费用为4元/米,弧线部分的装饰费用为9元/米,设花坛的面积与装饰总费用之比为![]() ,求
,求![]() 关于
关于![]() 的函数关系式,并求出
的函数关系式,并求出![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市组织500名志愿者参加敬老活动,为方便安排任务将所有志愿者按年龄(单位:岁)分组,得到的频率分布表如下.现要从年龄较小的第1,2,3组中用分层抽样的方法抽取6人担任联系人.
年龄(岁) | 频率 | |
第1组 |
| 0.1 |
第2组 |
| 0.1 |
第3组 |
| 0.4 |
第4组 |
| 0.3 |
第5组 |
| 0.1 |
(1)应分别在第1,2,3组中抽取志愿者多少人?
(2)从这6人中随机抽取2人担任本次活动的宣传员,求至少有1人年龄在第3组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的两个焦点与短轴的一个端点是等边三角形的三个顶点,且长轴长为4.
的两个焦点与短轴的一个端点是等边三角形的三个顶点,且长轴长为4.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)若![]() 是椭圆
是椭圆![]() 的左顶点,经过左焦点
的左顶点,经过左焦点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 与
与![]() 的面积之差的绝对值的最大值.(
的面积之差的绝对值的最大值.(![]() 为坐标原点)
为坐标原点)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数据![]() ,
,![]() ,
,![]() ,…,
,…,![]() 是杭州市100个普通职工的2016年10月份的收入(均不超过2万元),设这100个数据的中位数为
是杭州市100个普通职工的2016年10月份的收入(均不超过2万元),设这100个数据的中位数为![]() ,平均数为
,平均数为![]() ,方差为
,方差为![]() ,如果再加上马云2016年10月份的收入
,如果再加上马云2016年10月份的收入![]() (约100亿元),则相对于
(约100亿元),则相对于![]() 、
、![]() 、
、![]() ,这101个月收入数据( )
,这101个月收入数据( )
A.平均数可能不变,中位数可能不变,方差可能不变
B.平均数大大增大,中位数可能不变,方差也不变
C.平均数大大增大,中位数一定变大,方差可能不变
D.平均数大大增大,中位数可能不变,方差变大
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com