解:(1)

(x>-1),
由题意,f′(x)≥0在(-1,+∞)内恒成立,或f′(x)≤0在(-1,+∞)内恒成立.
若f′(x)≥0,则2x
2+2x+b≥0,即b≥-2x
2-2x=-2(x+

)
2+

恒成立,
显然,-2(x+

)
2+

在(-1,+∞)内的最大值为

,所以b

;
f′(x)≤0,则2x
2+2x+b≤0,
显然,该不等式在(-1,+∞)内不恒成立;
综上,所求b的取值范围为[

,+∞);
(2)由题意,f(1)是函数的最小值也是极小值.
因此f′(1)=2+

=0,解得b=-4,
经验证b=-4符合题意;
(3)首先研究f(x),g(x)在[0,1]上的性质,
由(1),当b=

时,函数f(x)=x
2+bln(x+1)在(-1,+∞)内单调递增,从从而f(x)在[0,1]上单调递增,
因此,f(x)在[0,1]上的最小值为f(0)=0,最大值为f(1)=1+

,
g′(x)=3(x
2-a
2),由a>1,知当x∈[0,1]时,g′(x)=3(x
2-a
2)<0,
因此g(x)=x
3-3a
2x+a
2-2a在[0,1]上单调递减.
∴g(x)
max=g(0)=a
2-2a,g(x)
min=g(1)=1-2a
2-2a,
∵a>1,∴g(x)
min=g(1)=1-2a
2-2a<0,
①若g(x)
max=g(0)=a
2-2a≥0,即a≥2时,两函数在[0,1]上有交点,此时a≥2显然满足条件;
②若g(x)
max=g(0)=a
2-2a<0,即1<a<2,f(x)的图象在上,g(x)的图象在下,
只需f(x)min-g(x)max<

,即f(0)-g(0)

,
即-(a
2-2a)

,
解得1+

.
综上,所求实数a的取值范围(1+

,+∞).
分析:(1)先求导:

,令导数大于或小于等于零,分离参数,转化为求函数的最值问题,从而求得b的取值范围;
(2)根据题意对f(x)定义域内的任意x,都有f(x)≥f(1),即说明f(1)是函数的最小值也是极小值,因此有f′(1)=0,从而求得b的值;
(3)要使不等式
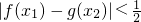
成立,即求两个函数的函数值相差最大不能超过

,因此利用导数分别求得两函数的值域即可求得实数a的取值范围.
点评:此题是个难题.本题主要考查用导数法研究函数的单调性,基本思路是:当函数为增函数时,导数大于等于零;当函数为减函数时,导数小于等于零,根据解题要求选择是否分离变量,体现了转化的思想和分类讨论以及数形结合的思想方法,同时考查了学生的灵活应用知识分析解决问题的能力和计算能力.

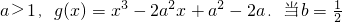 时,若存在x1,x2∈[0,1],使得
时,若存在x1,x2∈[0,1],使得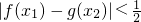 ,求实数a的取值范围.
,求实数a的取值范围. (x>-1),
(x>-1), )2+
)2+ 恒成立,
恒成立, )2+
)2+ 在(-1,+∞)内的最大值为
在(-1,+∞)内的最大值为 ,所以b
,所以b ;
; ,+∞);
,+∞); =0,解得b=-4,
=0,解得b=-4, 时,函数f(x)=x2+bln(x+1)在(-1,+∞)内单调递增,从从而f(x)在[0,1]上单调递增,
时,函数f(x)=x2+bln(x+1)在(-1,+∞)内单调递增,从从而f(x)在[0,1]上单调递增, ,
, ,即f(0)-g(0)
,即f(0)-g(0) ,
, ,
, .
. ,+∞).
,+∞). ,令导数大于或小于等于零,分离参数,转化为求函数的最值问题,从而求得b的取值范围;
,令导数大于或小于等于零,分离参数,转化为求函数的最值问题,从而求得b的取值范围;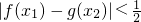 成立,即求两个函数的函数值相差最大不能超过
成立,即求两个函数的函数值相差最大不能超过 ,因此利用导数分别求得两函数的值域即可求得实数a的取值范围.
,因此利用导数分别求得两函数的值域即可求得实数a的取值范围.
