
【题目】已知当 ![]() 时,函数
时,函数 ![]() 的图象与
的图象与 ![]() 的图象有且只有一个交点,则正实数
的图象有且只有一个交点,则正实数 ![]() 的取值范围是 ( )
的取值范围是 ( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】B
【解析】根据题意,由于 ![]() 为正数,
为正数, ![]() 为二次函数,在区间
为二次函数,在区间 ![]() 为减函数,
为减函数, ![]() 为增函数,函数
为增函数,函数 ![]() 为增函数,分两种情况讨论:①当
为增函数,分两种情况讨论:①当 ![]() 时,有
时,有 ![]() 在区间
在区间 ![]() 上,
上, ![]() 为减函数,且其值域为
为减函数,且其值域为 ![]() ,函数
,函数 ![]() 为增函数,其值域为
为增函数,其值域为 ![]() ,此时两个函数的图象有一个交点,符合题意;②当
,此时两个函数的图象有一个交点,符合题意;②当 ![]() 时,有
时,有 ![]() ,
, ![]() 在区间
在区间 ![]() 为减函数,
为减函数, ![]() 为增函数,函数
为增函数,函数 ![]() 为增函数, 其值域为
为增函数, 其值域为 ![]() ,若两个函数的图象有一个交点,则有
,若两个函数的图象有一个交点,则有![]() ,解可得
,解可得 ![]() 或
或 ![]() ,由又
,由又 ![]() 为正数,则
为正数,则 ![]() ,综合可得
,综合可得 ![]() 的取值范围是
的取值范围是 ![]() ,
,
所以答案是:B.
【考点精析】解答此题的关键在于理解函数的零点与方程根的关系的相关知识,掌握二次函数的零点:(1)△>0,方程 有两不等实根,二次函数的图象与 轴有两个交点,二次函数有两个零点;(2)△=0,方程 有两相等实根(二重根),二次函数的图象与 轴有一个交点,二次函数有一个二重零点或二阶零点;(3)△<0,方程 无实根,二次函数的图象与 轴无交点,二次函数无零点.


科目:高中数学 来源: 题型:
【题目】下表是一位母亲给儿子作的成长记录:
年龄/周岁 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
身高/cm | 94.8 | 104.2 | 108.7 | 117.8 | 124.3 | 130.8 | 139.1 |
根据以上样本数据,她建立了身高 ![]() (cm)与年龄x(周岁)的线性回归方程为
(cm)与年龄x(周岁)的线性回归方程为 ![]() ,给出下列结论:
,给出下列结论:
①y与x具有正的线性相关关系;
②回归直线过样本的中心点(42,117.1);
③儿子10岁时的身高是 ![]() cm;
cm;
④儿子年龄增加1周岁,身高约增加 ![]() cm.
cm.
其中,正确结论的个数是
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() 的离心率为
的离心率为 ![]() ,且它的一个焦点
,且它的一个焦点 ![]() 的坐标为
的坐标为 ![]() .
.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)设过焦点 ![]() 的直线与椭圆相交于
的直线与椭圆相交于 ![]() 两点,
两点, ![]() 是椭圆上不同于
是椭圆上不同于 ![]() 的动点,试求
的动点,试求 ![]() 的面积的最大值.
的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
为了保护环境,发展低碳经济,某单位在政府部门的支持下,进行技术攻关,采用了新工艺,新上了把二氧化碳转化为一种可利用的化工产品的项目.经测算,月处理成本![]() (元)与月处理量
(元)与月处理量![]() (吨)之间的函数关系可以近似的表示为:
(吨)之间的函数关系可以近似的表示为: ,且每处理一吨二氧化碳可得到能利用的化工产品价值为200元,若该项目不获利,政府将补贴.
,且每处理一吨二氧化碳可得到能利用的化工产品价值为200元,若该项目不获利,政府将补贴.
(I)当![]() 时,判断该项目能否获利?如果获利,求出最大利润;如果不获利,则政府每月至少需要补贴多少元才能使该项目不亏损;
时,判断该项目能否获利?如果获利,求出最大利润;如果不获利,则政府每月至少需要补贴多少元才能使该项目不亏损;
(II)该项目每月处理量为多少吨时,才能使每吨的平均处理成本最低?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某游艇制造厂研发了一种新游艇,今年前5个月的产量如下:

(1)设![]() 关于
关于![]() 的回归直线方程为
的回归直线方程为![]() 现根据表中数据已经正确计算出了
现根据表中数据已经正确计算出了![]() 的值为
的值为![]() ,试求
,试求![]() 的值,并估计该厂
的值,并估计该厂![]() 月份的产量;(计算结果精确到
月份的产量;(计算结果精确到![]() )
)
(Ⅱ)质检部门发现该厂![]() 月份生产的游艇都存在质量问题,要求厂家召回;现有一旅游公司曾向该厂购买了今年前两个月生产的游艇
月份生产的游艇都存在质量问题,要求厂家召回;现有一旅游公司曾向该厂购买了今年前两个月生产的游艇![]() 艘,求该旅游公司有游艇被召回的概率.
艘,求该旅游公司有游艇被召回的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)当![]() 时,
时,![]() 恒成立,求实数m的取值范围;
恒成立,求实数m的取值范围;
(2)是否存在整数a、b(其中a、b是常数,且a<b),使得关于x的不等式![]() 的解集为
的解集为![]() ?若存在,求出a、b的值,若不存在,请说明理由.
?若存在,求出a、b的值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面程序框图中,若输入互不相等的三个正实数a,b,c(abc≠0),要求判断△ABC的形状,则空白的判断框应填入( ) 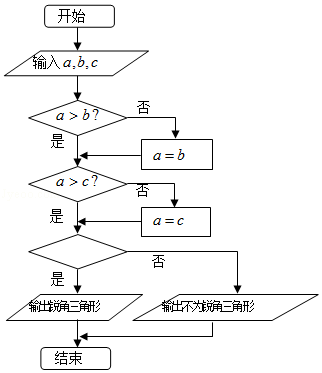
A.a2+b2>c2?
B.a2+c2>b2?
C.b2+c2>a2?
D.b2+a2=c2?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com