
| |||||||||||
(1) |
解析:由已知Sn+1=2Sn+n+5,得n≥2时,Sn=2sn-l+n+4. 两式相减,得Sn+1-Sn=2(Sn-Sn-1)+1 即an+1=2an+1,从而an+1+1=2(an+1). 当n=1时,S2=2S1+1+5,∴a1+a2=2a1+6. 又a1=5,∴a2=11,从而a2+1=2(a1+1). 故总有 an+1+1=2(an+1),n∈N*. 又∵a1=5,∴an+1≠0,从而 即{an+1}是以a1+1=6为首项,2为公比的等比数列. |
(2) |
解析:由(1)得an=3×2n-1. ∵f(x)=a1x+a2x2+…anxn, ∴ 从而 =(3×2-1)+2(3×22-1)+…+n(3×2n-1) =3(2+2×22+…+n×2n)-(1+2+…+n) =3[n×2n+1-(2+…+2n)]- =3[n×2n+1-2n+1+2]- =3(n-1)·2n+1- 点评:本题要注意在n≥2时,an+1+1=2(an+1)成立,不包括a2+1=2(a1+1),需补充验证. |


科目:高中数学 来源:福建省三明一中2008-2009学年高一下学期第一次月考数学试题 题型:044
已知数列{an}的首项a1=1,数列![]() 是公比为4的等比数列
是公比为4的等比数列
(1)求数列{an}的通项公式;
(2)记数列{an}的前n项的和为Sn,求![]()
查看答案和解析>>
科目:高中数学 来源:山东省淄博市2010届高三上学期期末考试文科数学试卷 题型:044
已知数列{an}的首项a1=5,前n项和为Sn,且Sn+1=2Sn+n+5(n∈N*).
(Ⅰ)设bn=an+1,求数列{bn}的通项公式;
(Ⅱ)求数列{an}的前n项和Sn.
查看答案和解析>>
科目:高中数学 来源:江苏省无锡市洛社中学2012届高三上学期12月月考数学试题 题型:044
已知数列{an}的首项a1=![]() ,an+1=
,an+1=![]() ,n=1,2,….
,n=1,2,….
(1)求证:数列 为等比数列;
为等比数列;
(2)记Sn=![]() +
+![]() +…
+…![]() ,若Sn<100,求最大正整数n.
,若Sn<100,求最大正整数n.
(3)是否存在互不相等的正整数m,s,n,使m,s,n成等差数列且am-1,a5-1,an-1成等比数列,如果存在,请给出证明;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2012届江西省上饶市高三第二次模拟考试理科数学试卷(解析版) 题型:解答题
(12分)已知数列{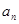 }的首项a1=5,前n项和为Sn,且Sn+1=2Sn+n+5
}的首项a1=5,前n项和为Sn,且Sn+1=2Sn+n+5
(1)求证{1+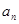 }为等比数列,并求数列{
}为等比数列,并求数列{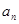 }的通项公式;
}的通项公式;
(2)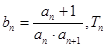 是数列{
是数列{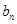 }前n项和,求Tn.
}前n项和,求Tn.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com