
����Ŀ����ƽ��ֱ������ϵxOy�У���֪ԲC1����x+1��2+y2=1��ԲC2����x��3��2+��y��4��2=1��
����������C1����1��0����ֱ��l��ԲC2�صõ��ҳ�Ϊ ![]() ����ֱ��l�ķ��̣�
����ֱ��l�ķ��̣�
����ԲD����1Ϊ�뾶��Բ����ԲC3����x+1��2+y2=9���ƶ��Ķ�Բ����ԲD������һ��P�ֱ���ԲC1����������PE��PF���е�ΪE��F���� ![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��������ԲCͬʱƽ��ԲC1���ܳ���ԲC2���ܳ�����ԲC�Ƿ����㣿�������������������ꣻ������������˵�����ɣ�
���𰸡��⣺������ֱ��l�ķ���Ϊy=k��+1������kx��y+k=0��
��Ϊֱ��l��ԲC2�صõ��ҳ�Ϊ ![]() ����ԲC2�İ뾶Ϊ1��
����ԲC2�İ뾶Ϊ1��
����Բ��C2��3��4����l��kx��y+k=0�ľ���Ϊ ![]() ��
��
����12k2��25k+12=0�����k= ![]() ��k=
��k= ![]() ��
��
����ֱ��l����Ϊ4x��3y+4=0��3x��4y+3=0
����ԲD��Բ���ڶ�Բ��x+1��2+y2=9���ƶ����뾶Ϊ1��Բ
���EC1F=2��������Rt��PC1E�� ![]() ��
��
�� ![]() ��
��
�� ![]()
��Բ�ļ������ʵã�|DC1|��r��|PC1|��|DC1|+r����2��|PC1|��4�� ![]()
�� ![]() �����ֵΪ
�����ֵΪ ![]() ����СֵΪ
����СֵΪ ![]() ��
��
�� ![]() ��
��
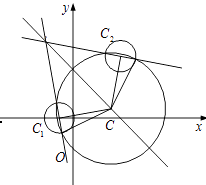
������Բ��C��x��y���������⣬��CC1=CC2 ��
�� ![]() ��
��
�����x+y��3=0������ԲԲ��C�ڶ�ֱ��x+y��3=0���˶���
��C��m.3��m������ԲC�İ뾶Ϊ ![]() =
= ![]() ��
��
���Ƕ�ԲC�ķ���Ϊ��x��m��2+��y��3+m��2=1+��m+1��2+��3��m��2 ��
��������x2+y2��6y��2��2m��x��y+1��=0��
�� ![]() ��
�� 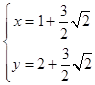 ��
�� 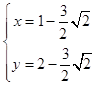
���Զ��������Ϊ��1�� ![]() ��2��
��2�� ![]() ������1+
������1+ ![]() ��2+
��2+ ![]() ��
��

��������������ֱ��l�ķ���Ϊy=k��+1��������ֱ��l��ԲC2�صõ��ҳ�Ϊ ![]() �����ù��ɶ��������k��������ֱ��l�ķ��̣�����ԲD��Բ���ڶ�Բ��x+1��2+y2=9���ƶ����뾶Ϊ1��Բ����Բ�ļ������ʵã�|DC1|��r��|PC1|��|DC1|+r����2��|PC1|��4��
�����ù��ɶ��������k��������ֱ��l�ķ��̣�����ԲD��Բ���ڶ�Բ��x+1��2+y2=9���ƶ����뾶Ϊ1��Բ����Բ�ļ������ʵã�|DC1|��r��|PC1|��|DC1|+r����2��|PC1|��4�� ![]() ��������������������ʽ��������
��������������������ʽ�������� ![]() ��ȡֵ��Χ������ȷ����ԲԲ��C�ڶ�ֱ��x+y��3=0���˶��������ԲC�ķ��̣����ɵó����ۣ�
��ȡֵ��Χ������ȷ����ԲԲ��C�ڶ�ֱ��x+y��3=0���˶��������ԲC�ķ��̣����ɵó����ۣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ȫ��U=R������A={x|1��2x��1��5}��B={y|y=�� ![]() ��x �� x�ݩ�2}��
��x �� x�ݩ�2}��
��1����UA����B��
��2��������C={x|a��1��x��a��1}����CA����ʵ��a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ʵ��a��b��c����loga3��logb3��logc3�������й�ϵ�в����ܳ����ģ� ��
A.a��b��c
B.b��a��c
C.c��b��a
D.a��c��b
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������ڹ۲�õ����ڽ�ͨ��æ��ʱ���ڣ�ij��·�������ij�����y��ǧ��/Сʱ����������ƽ���ٶȦԣ�ǧ��/Сʱ��֮��ĺ�����ϵΪ��y= ![]() ���ԣ�0����
���ԣ�0����
��1���ڸ�ʱ���ڣ���������ƽ���ٶȦ�Ϊ����ʱ������������������Ϊ���٣�������������ʽ��
��2����Ҫ���ڸ�ʱ���ڳ���������10ǧ��/Сʱ����������ƽ���ٶ�Ӧ��ʲô��Χ�ڣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪{an}�ǵȲ����У�{bn}�ǵȱ����У�SnΪ����{an}��ǰn��ͣ�a1=b1=1����b3S3=36��b2S2=8��n��N+����
��1����an��bn��
��2����an��an+1 �� ������ ![]() ��ǰn���Tn ��
��ǰn���Tn ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=sin����x+�գ����أ�0��|��|�� ![]() ���IJ���ͼ����ͼ��ʾ����y=f��x����ͼ�����y=cos2xͼ�� ��
���IJ���ͼ����ͼ��ʾ����y=f��x����ͼ�����y=cos2xͼ�� �� 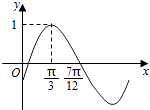
A.����ƽ�� ![]() �����ȵ�λ
�����ȵ�λ
B.����ƽ�� ![]() �����ȵ�λ
�����ȵ�λ
C.����ƽ�� ![]() �����ȵ�λ
�����ȵ�λ
D.����ƽ�� ![]() �����ȵ�λ
�����ȵ�λ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������Ʒ�ڹ�ȥһ��ʱ���ڵļ۸�������ͼ��ʾ������ij�˳����ʽ�120��Ԫ����������t1��t4������ʱ��������������Ʒ���������ܹ������ɽ����������ú��Բ��ƣ�����ô�����е��ʽ����ɱ�Ϊ�� �� 
A.120��Ԫ
B.160��Ԫ
C.220��Ԫ
D.240��Ԫ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������ij�豸��ʹ������x����֧����ά����y����Ԫ���������µ�ͳ�����ϣ�
x | 1 | 2 | 3 | 4 | 5 |
y | 5 | 6 | 7 | 8 | 10 |
�����Ͽ�֪y��x��������ع�ϵ�������Իع鷽��Ϊ ![]() �������ʹ������Ϊ20��ʱ��ά����ԼΪ�� ��
�������ʹ������Ϊ20��ʱ��ά����ԼΪ�� ��
A.26.2
B.27
C.27.6
D.28.2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�ֲ�Ʒ��Լ�����̸����������ص�����������ó���ͼ���ֲ�Ʒ����������Ƶ�ʷֲ�ֱ��ͼ�� 
��1����ͼ��a��ֵ������������������������
��2��ij�գ������̹���130�����ֲ�Ʒ�����ݽ����г����飬����ÿ�۳�1���ܻ���30Ԫ��δ�۳��IJ��֣�ÿ������20Ԫ���赱���������Ϊx����100��x��150����������ΪSԪ��
��������S��ʾΪx�ĺ�����
����������ֱ��ͼ���Ƶ��촿����S������3400Ԫ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com