
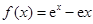 .
.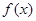 的最小值;
的最小值;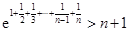
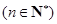 ;
;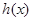 与
与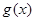 定义域上的任意实数
定义域上的任意实数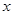 ,若存在常数
,若存在常数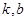 ,使得
,使得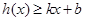 和
和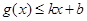 都成立,则称直线
都成立,则称直线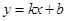 为函数
为函数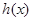 与
与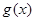 的“分界线”.设函数
的“分界线”.设函数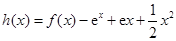 ,
,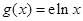 ,
,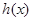 与
与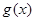 是否存在“分界线”?若存在,求出
是否存在“分界线”?若存在,求出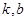 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.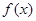 的最小值为
的最小值为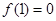 ;(Ⅱ)详见解析;(Ⅲ)
;(Ⅱ)详见解析;(Ⅲ)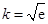 ,
,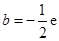
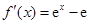 ,由此可得函数
,由此可得函数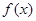 在
在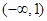 上递减,
上递减,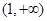 上递增,
上递增,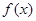 的最小值为
的最小值为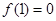 .
. 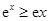 .这个不等式如何用?结合所在证的不等式可以看出,可以两端同时乘以
.这个不等式如何用?结合所在证的不等式可以看出,可以两端同时乘以 变形为:
变形为: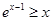 ,把
,把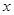 换成
换成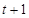 得
得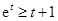 ,在这个不等式中令
,在这个不等式中令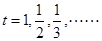 然后将各不等式相乘即得.
然后将各不等式相乘即得.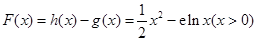 .通过求导可得当
.通过求导可得当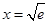 时
时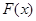 取得最小值0,这说明
取得最小值0,这说明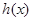 与
与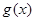 的图象在
的图象在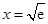 处有公共点
处有公共点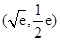 .如果它们存在分界线,则这条分界线必过该点.所以设
.如果它们存在分界线,则这条分界线必过该点.所以设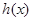 与
与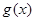 的“分界线”方程为
的“分界线”方程为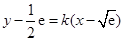 .由于
.由于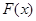 的最小值为0,所以
的最小值为0,所以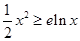 ,所以分界线必满足
,所以分界线必满足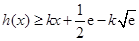 和
和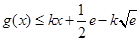 .下面就利用这两个不等式来确定
.下面就利用这两个不等式来确定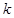 的值.
的值.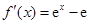 ,令
,令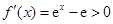 ,解得
,解得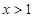 ,
,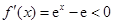 ,解得
,解得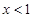 ,
,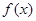 在
在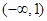 上递减,
上递减,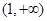 上递增,
上递增,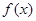 的最小值为
的最小值为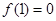 . 3分
. 3分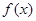 在
在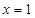 取得最小值,所以
取得最小值,所以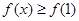 ,即
,即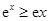
 得
得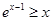 ,把
,把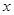 换成
换成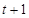 得
得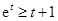 ,当且仅当
,当且仅当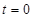 时等号成立.
时等号成立.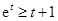 得,
得,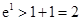 ,
,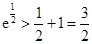 ,
,  ,
, 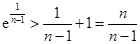 ,
,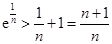 .
.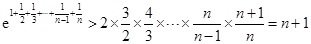 . 9分
. 9分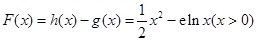 .
.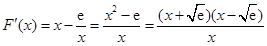 .
.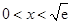 时,
时, ;当
;当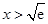 时,
时,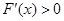 .
.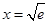 时
时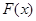 取得最小值0,则
取得最小值0,则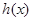 与
与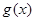 的图象在
的图象在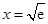 处有公共点
处有公共点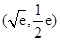 .
.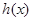 与
与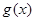 存在 “分界线”,方程为
存在 “分界线”,方程为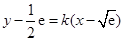 .
.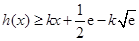 在
在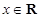 恒成立,
恒成立,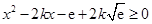 在
在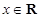 恒成立.
恒成立.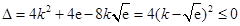 成立.因此
成立.因此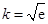 .
.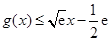
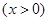 成立.
成立.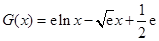 ,
,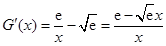 .
.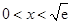 时,
时,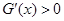 ;当
;当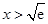 时,
时,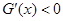 .
.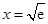 时
时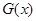 取得最大值0,则
取得最大值0,则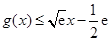
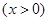 成立.
成立.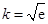 ,
,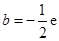 . 14分
. 14分

科目:高中数学 来源:不详 题型:解答题
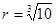 毫米,滴管内液体忽略不计.
毫米,滴管内液体忽略不计.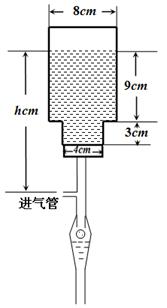
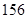 分钟滴完,问每分钟应滴下多少滴?
分钟滴完,问每分钟应滴下多少滴?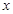 (单位:分钟),瓶内液面与进气管的距离为
(单位:分钟),瓶内液面与进气管的距离为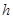 (单位:厘米),已知当
(单位:厘米),已知当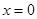 时,
时,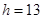 .试将
.试将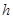 表示为
表示为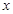 的函数.(注:
的函数.(注: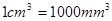 )
)查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 (单位:辆/千米)的函数.当桥上的的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时,研究表明:当
(单位:辆/千米)的函数.当桥上的的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时,研究表明:当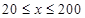 时,车流速度
时,车流速度 是车流密度x的一次函数.
是车流密度x的一次函数. 时,求函数
时,求函数 的表达式;
的表达式; 为多大时,车流量(单位时间内通过桥上某观察点的车辆数,单位:辆/每小时)
为多大时,车流量(单位时间内通过桥上某观察点的车辆数,单位:辆/每小时) 可以达到最大,并求出最大值(精确到1辆/小时).
可以达到最大,并求出最大值(精确到1辆/小时).查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
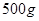 ,按每年
,按每年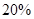 衰减.
衰减.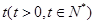 年后,这种放射性元素的质量
年后,这种放射性元素的质量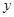 与
与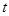 的函数关系式;
的函数关系式; 时所经历的时间).(
时所经历的时间).(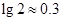 )
)查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 ,从A到B的映射
,从A到B的映射 在映射下,B中的元素为(4,2)对应的A中元素为 ( )
在映射下,B中的元素为(4,2)对应的A中元素为 ( )| A.(4,2) | B.(1,3) | C.(6,2) | D.(3,1) |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
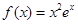 既无最小值也无最大值;
既无最小值也无最大值;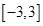 上随机取一个数
上随机取一个数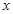 ,使得
,使得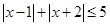 成立的概率为
成立的概率为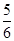 ;
;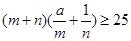 对任意正实数
对任意正实数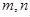 恒成立,则正实数
恒成立,则正实数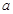 的最小值为16;
的最小值为16;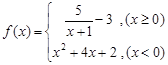 ,若方程
,若方程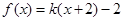 恰有三个不同的实根,则实数
恰有三个不同的实根,则实数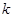 的取值范围是
的取值范围是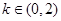 ;以上正确的命题序号是:_______.
;以上正确的命题序号是:_______.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com