
分析 先求出b=2,c=3,从而求出M=$[\begin{array}{l}{1}&{2}\\{3}&{2}\end{array}]$,由此利用矩阵M的特征多项式能求出矩阵M及另一个特征值λ2和特征向量$\overrightarrow{{e}_{2}}$.
解答 解:∵矩阵M=$[\begin{array}{l}{1}&{b}\\{c}&{2}\end{array}]$有特征值λ1=4及对应的一个特征向量$\overrightarrow{{e}_{1}}$=$[\begin{array}{l}{2}\\{3}\end{array}]$,
∴$[\begin{array}{l}{1}&{b}\\{c}&{2}\end{array}][\begin{array}{l}{2}\\{3}\end{array}]$=$[\begin{array}{l}{8}\\{12}\end{array}]$,
∴$\left\{\begin{array}{l}{2+3b=8}\\{2c+6=12}\end{array}\right.$,
解得b=2,c=3,
∴M=$[\begin{array}{l}{1}&{2}\\{3}&{2}\end{array}]$.
矩阵M的特征多项式为f(λ)=(λ-1)(λ-2)-6=(λ+1)(λ-4)=0,
解得λ1=4,λ2=-1,
当λ2=-1时,设$\overrightarrow{{e}_{2}}=[\begin{array}{l}{{a}_{1}}\\{{a}_{2}}\end{array}]$,则$[\begin{array}{l}{1}&{2}\\{3}&{2}\end{array}][\begin{array}{l}{{a}_{1}}\\{{a}_{2}}\end{array}]$=$[\begin{array}{l}{-{a}_{1}}\\{-{a}_{2}}\end{array}]$,
解得a2=-a1,
令a1=1,得$\overrightarrow{{e}_{2}}$=$[\begin{array}{l}{1}\\{-1}\end{array}]$.(答案不唯一).
点评 本题考查矩阵及特征值和特征向量的求法,是基础题,解题时要认真审题,注意矩阵运算性质的合理运用.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{3}{5}$ | C. | $\frac{1}{3}$ | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
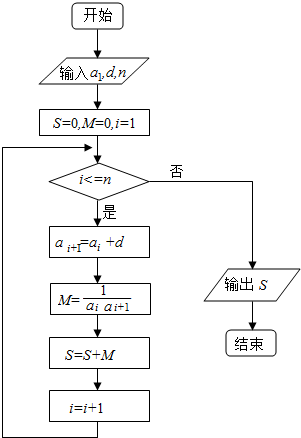
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,D是△ABC外接圆上的一点,弦AD与BC交于点E,且AB=AC=6,AE=4.
如图,D是△ABC外接圆上的一点,弦AD与BC交于点E,且AB=AC=6,AE=4.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 与a,b都相交 | B. | 与a,b都垂直 | C. | 与a平行,与b垂直 | D. | 与a,b都平行 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com